makeMoE: 從零開始實現稀疏專家混合語言模型
TL;DR:本部落格將逐步介紹如何從零開始實現一個稀疏專家混合語言模型。這篇部落格的靈感主要來自於 Andrej Karpathy 的專案“makemore”,並借鑑了該實現中的許多可重用元件。與 makemore 一樣,makeMoE 也是一個自迴歸字元級語言模型,但它使用了上述的稀疏專家混合架構。部落格的其餘部分將重點介紹該架構的關鍵元素以及它們的實現方式。我的目標是讓您在閱讀完這篇部落格並逐步檢視程式碼庫中的程式碼後,能夠直觀地理解它的工作原理。
GitHub 倉庫在此處提供端到端實現:https://github.com/AviSoori1x/makeMoE/tree/main

隨著 Mixtral 的釋出以及 GPT-4 可能是一個專家混合大型語言模型的說法,人們對這種模型架構產生了濃厚的興趣。然而,在稀疏專家混合語言模型中,大部分元件與傳統 Transformer 共享。儘管看似簡單,但經驗證據表明,訓練穩定性是這些模型的主要問題之一。像這樣的可修改小規模實現可能有助於快速試驗新方法。
在此次實現中,我對 makemore 架構進行了一些重大修改:
- 稀疏專家混合代替了單一的前饋神經網路。
- Top-k 門控和帶噪聲的 Top-k 門控實現。
- 初始化 - 此處使用 Kaiming He 初始化,但本 Notebook 的重點是可修改性,因此您可以換用 Xavier/Glorot 初始化等進行嘗試。
然而,以下內容與 makemore 保持不變:
- 資料集、預處理(分詞)以及 Andrej 最初選擇的語言建模任務——生成類似莎士比亞的文字。
- 因果自注意力實現
- 訓練迴圈
- 推理邏輯
我們開始吧!
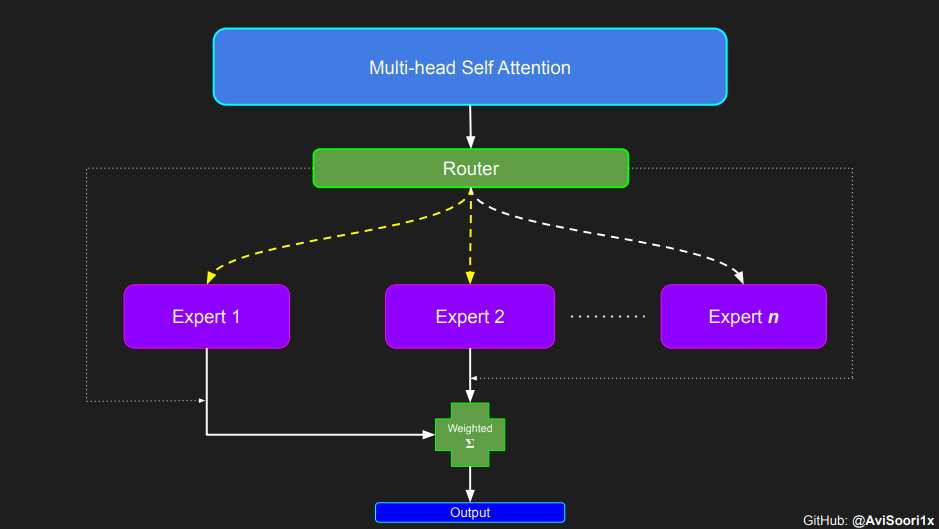
稀疏專家混合語言模型,正如預期的那樣,依賴於自注意力機制進行上下文理解。接下來,我們將深入探討專家混合模組的複雜性。首先,讓我們深入瞭解自注意力以重新整理我們的理解。
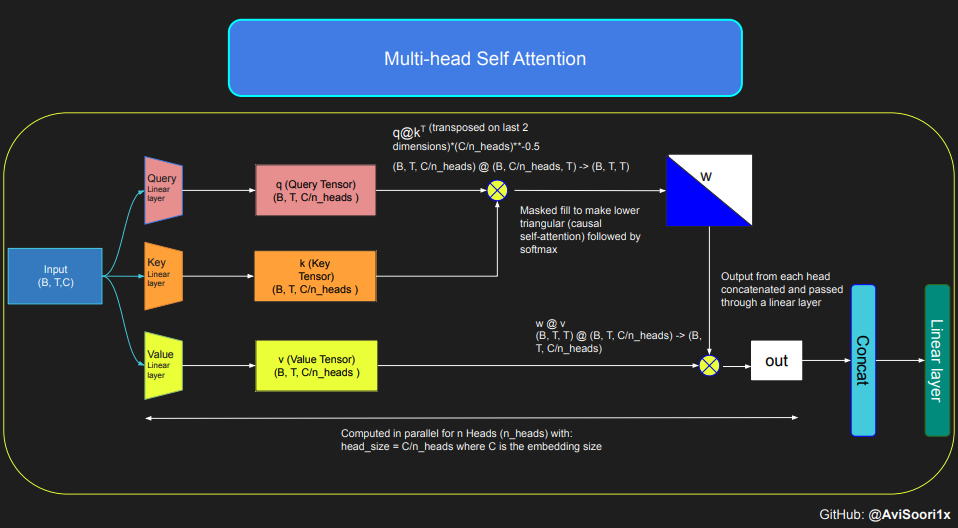
理解因果縮放點積自注意力的直覺
所提供的程式碼演示了自注意力的機制和基本概念,特別關注經典的縮放點積自注意力。在此變體中,查詢、鍵和值矩陣都源自相同的輸入序列。為了確保自迴歸語言生成過程的完整性,特別是在僅解碼器模型中,程式碼實現了掩碼。這種掩碼技術至關重要,因為它會遮蓋當前標記位置之後的所有資訊,從而將模型的注意力僅引導到序列的先前部分。這種注意力機制被稱為因果自注意力。值得注意的是,稀疏專家混合模型不限於僅解碼器 Transformer 架構。事實上,該領域的大部分重要工作,特別是 Shazeer 等人的工作,都圍繞 T5 架構,該架構包含 Transformer 模型中的編碼器和解碼器元件。
#This code is borrowed from Andrej Karpathy's makemore repository linked in the repo.
The self attention layers in Sparse mixture of experts models are the same as
in regular transformer models
torch.manual_seed(1337)
B,T,C = 4,8,32 # batch, time, channels
x = torch.randn(B,T,C)
# let's see a single Head perform self-attention
head_size = 16
key = nn.Linear(C, head_size, bias=False)
query = nn.Linear(C, head_size, bias=False)
value = nn.Linear(C, head_size, bias=False)
k = key(x) # (B, T, 16)
q = query(x) # (B, T, 16)
wei = q @ k.transpose(-2, -1) # (B, T, 16) @ (B, 16, T) ---> (B, T, T)
tril = torch.tril(torch.ones(T, T))
#wei = torch.zeros((T,T))
wei = wei.masked_fill(tril == 0, float('-inf'))
wei = F.softmax(wei, dim=-1) #B,T,T
v = value(x) #B,T,H
out = wei @ v # (B,T,T) @ (B,T,H) -> (B,T,H)
out.shape
torch.Size([4, 8, 16])
因果自注意力與多頭因果自注意力的程式碼可以組織如下。多頭自注意力並行應用多個注意力頭,每個頭關注通道(嵌入維度)的不同部分。多頭自注意力由於其固有的並行實現,本質上改進了學習過程並提高了模型訓練效率。請注意,我在整個實現中使用了 dropout 進行正則化,即防止過擬合。
#Causal scaled dot product self-Attention Head
n_embd = 64
n_head = 4
n_layer = 4
head_size = 16
dropout = 0.1
class Head(nn.Module):
""" one head of self-attention """
def __init__(self, head_size):
super().__init__()
self.key = nn.Linear(n_embd, head_size, bias=False)
self.query = nn.Linear(n_embd, head_size, bias=False)
self.value = nn.Linear(n_embd, head_size, bias=False)
self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))
self.dropout = nn.Dropout(dropout)
def forward(self, x):
B,T,C = x.shape
k = self.key(x) # (B,T,C)
q = self.query(x) # (B,T,C)
# compute attention scores ("affinities")
wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)
wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B, T, T)
wei = F.softmax(wei, dim=-1) # (B, T, T)
wei = self.dropout(wei)
# perform the weighted aggregation of the values
v = self.value(x) # (B,T,C)
out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C)
return out
多頭自注意力實現如下
#Multi-Headed Self Attention
class MultiHeadAttention(nn.Module):
""" multiple heads of self-attention in parallel """
def __init__(self, num_heads, head_size):
super().__init__()
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])
self.proj = nn.Linear(n_embd, n_embd)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
out = torch.cat([h(x) for h in self.heads], dim=-1)
out = self.dropout(self.proj(out))
return out
建立一個專家模組,即一個簡單的多層感知器
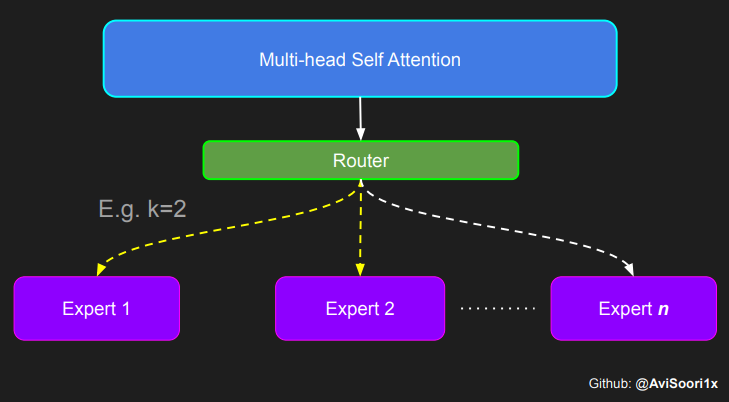
在稀疏專家混合(MoE)架構中,每個 Transformer 塊內的自注意力機制保持不變。然而,每個塊的結構發生了一個顯著變化:標準的 Feed-forward 神經網路被替換為幾個稀疏啟用的 Feed-forward 網路,這些網路被稱為專家。“稀疏啟用”指的是序列中的每個 token 只被路由到這些專家中的有限數量——通常是一到兩個——而不是全部可用專家。這有助於訓練和推理速度,因為在每次前向傳播中只啟用少數專家。然而,所有專家都必須駐留在 GPU 記憶體中,當總引數量達到數千億甚至數萬億時,這會帶來有趣的部署問題。
#Expert module
class Expert(nn.Module):
""" An MLP is a simple linear layer followed by a non-linearity i.e. each Expert """
def __init__(self, n_embd):
super().__init__()
self.net = nn.Sequential(
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd),
nn.Dropout(dropout),
)
def forward(self, x):
return self.net(x)
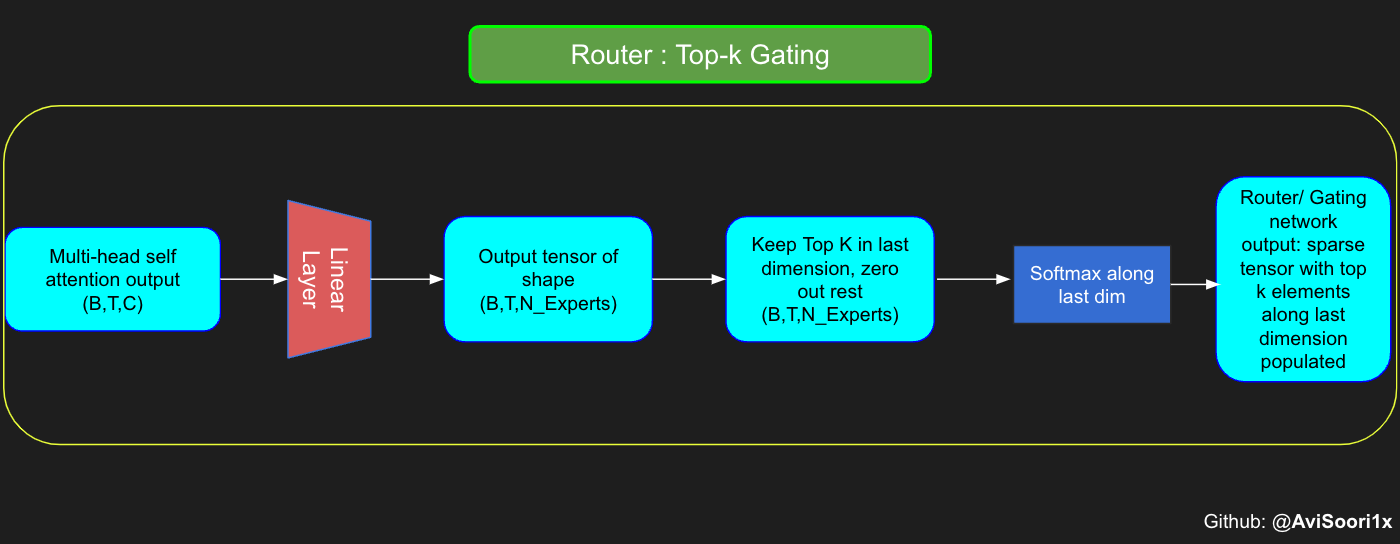
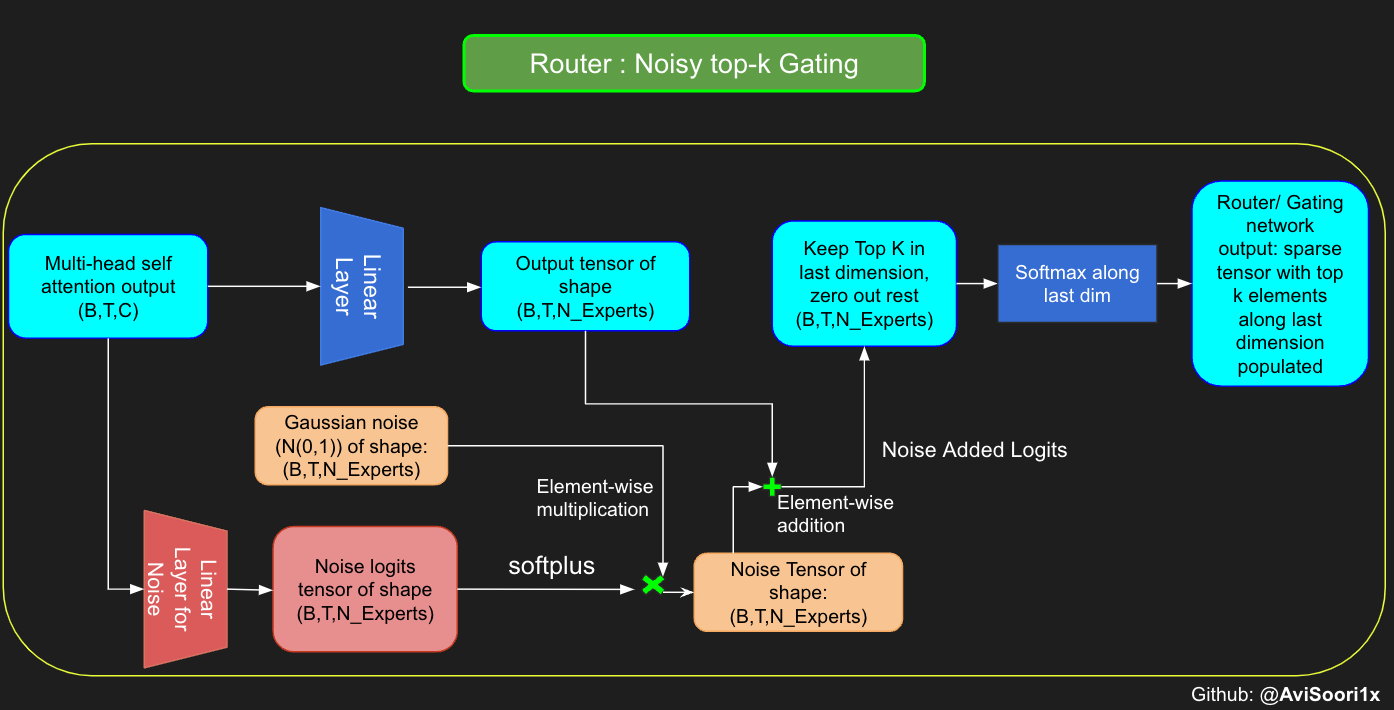
透過示例理解 Top-k 門控的直覺
門控網路,也稱為路由器,決定了哪個專家網路接收來自多頭注意力的每個 token 的輸出。讓我們考慮一個簡單的例子:假設有 4 個專家,並且 token 將被路由到前 2 個專家。最初,我們透過線性層將 token 輸入到門控網路。該層將輸入張量從 (2, 4, 32) 的形狀(表示批處理大小、標記、n_embed,其中 n_embed 是輸入的通道維度)投影到 (2, 4, 4) 的新形狀,這對應於(批處理大小、標記、專家數量),其中專家數量是專家網路的數量。在此之後,我們確定沿最後一個維度的前 k=2 個最高值及其各自的索引。
#Understanding how gating works
num_experts = 4
top_k=2
n_embed=32
#Example multi-head attention output for a simple illustrative example, consider n_embed=32, context_length=4 and batch_size=2
mh_output = torch.randn(2, 4, n_embed)
topkgate_linear = nn.Linear(n_embed, num_experts) # nn.Linear(32, 4)
logits = topkgate_linear(mh_output)
top_k_logits, top_k_indices = logits.topk(top_k, dim=-1) # Get top-k experts
top_k_logits, top_k_indices
#output:
(tensor([[[ 0.0246, -0.0190],
[ 0.1991, 0.1513],
[ 0.9749, 0.7185],
[ 0.4406, -0.8357]],
[[ 0.6206, -0.0503],
[ 0.8635, 0.3784],
[ 0.6828, 0.5972],
[ 0.4743, 0.3420]]], grad_fn=<TopkBackward0>),
tensor([[[2, 3],
[2, 1],
[3, 1],
[2, 1]],
[[0, 2],
[0, 3],
[3, 2],
[3, 0]]]))
透過僅保留沿最後一個維度中各自索引的前 k 個值來獲得稀疏門控輸出。其餘部分填充為“-inf”,並透過 softmax 啟用。這將“-inf”值推向零,使前兩個值更加突出並和為 1。這個和為 1 有助於專家輸出的加權。
zeros = torch.full_like(logits, float('-inf')) #full_like clones a tensor and fills it with a specified value (like infinity) for masking or calculations.
sparse_logits = zeros.scatter(-1, top_k_indices, top_k_logits)
sparse_logits
#output
tensor([[[ -inf, -inf, 0.0246, -0.0190],
[ -inf, 0.1513, 0.1991, -inf],
[ -inf, 0.7185, -inf, 0.9749],
[ -inf, -0.8357, 0.4406, -inf]],
[[ 0.6206, -inf, -0.0503, -inf],
[ 0.8635, -inf, -inf, 0.3784],
[ -inf, -inf, 0.5972, 0.6828],
[ 0.3420, -inf, -inf, 0.4743]]], grad_fn=<ScatterBackward0>)
gating_output= F.softmax(sparse_logits, dim=-1)
gating_output
#ouput
tensor([[[0.0000, 0.0000, 0.5109, 0.4891],
[0.0000, 0.4881, 0.5119, 0.0000],
[0.0000, 0.4362, 0.0000, 0.5638],
[0.0000, 0.2182, 0.7818, 0.0000]],
[[0.6617, 0.0000, 0.3383, 0.0000],
[0.6190, 0.0000, 0.0000, 0.3810],
[0.0000, 0.0000, 0.4786, 0.5214],
[0.4670, 0.0000, 0.0000, 0.5330]]], grad_fn=<SoftmaxBackward0>)
泛化和模組化上述程式碼,併為負載均衡新增帶噪聲的 Top-k 門控
# First define the top k router module
class TopkRouter(nn.Module):
def __init__(self, n_embed, num_experts, top_k):
super(TopkRouter, self).__init__()
self.top_k = top_k
self.linear =nn.Linear(n_embed, num_experts)
def forward(self, mh_ouput):
# mh_ouput is the output tensor from multihead self attention block
logits = self.linear(mh_output)
top_k_logits, indices = logits.topk(self.top_k, dim=-1)
zeros = torch.full_like(logits, float('-inf'))
sparse_logits = zeros.scatter(-1, indices, top_k_logits)
router_output = F.softmax(sparse_logits, dim=-1)
return router_output, indices
讓我們用一些樣本輸入來測試功能
#Testing this out:
num_experts = 4
top_k = 2
n_embd = 32
mh_output = torch.randn(2, 4, n_embd) # Example input
top_k_gate = TopkRouter(n_embd, num_experts, top_k)
gating_output, indices = top_k_gate(mh_output)
gating_output.shape, gating_output, indices
#And it works!!
#output
(torch.Size([2, 4, 4]),
tensor([[[0.5284, 0.0000, 0.4716, 0.0000],
[0.0000, 0.4592, 0.0000, 0.5408],
[0.0000, 0.3529, 0.0000, 0.6471],
[0.3948, 0.0000, 0.0000, 0.6052]],
[[0.0000, 0.5950, 0.4050, 0.0000],
[0.4456, 0.0000, 0.5544, 0.0000],
[0.7208, 0.0000, 0.0000, 0.2792],
[0.0000, 0.0000, 0.5659, 0.4341]]], grad_fn=<SoftmaxBackward0>),
tensor([[[0, 2],
[3, 1],
[3, 1],
[3, 0]],
[[1, 2],
[2, 0],
[0, 3],
[2, 3]]]))
儘管最近釋出的 Mixtral 論文並未提及,但我相信帶噪聲的 top-k 門控是訓練 MoE 模型的重要工具。本質上,你不想讓所有 token 都發送到同一組“偏愛”的專家。你需要一個精細的探索與利用平衡。為此,為了負載均衡,向門控線性層的 logits 新增標準正態噪聲會很有幫助。這使得訓練更有效率。
#Changing the above to accomodate noisy top-k gating
class NoisyTopkRouter(nn.Module):
def __init__(self, n_embed, num_experts, top_k):
super(NoisyTopkRouter, self).__init__()
self.top_k = top_k
#layer for router logits
self.topkroute_linear = nn.Linear(n_embed, num_experts)
self.noise_linear =nn.Linear(n_embed, num_experts)
def forward(self, mh_output):
# mh_ouput is the output tensor from multihead self attention block
logits = self.topkroute_linear(mh_output)
#Noise logits
noise_logits = self.noise_linear(mh_output)
#Adding scaled unit gaussian noise to the logits
noise = torch.randn_like(logits)*F.softplus(noise_logits)
noisy_logits = logits + noise
top_k_logits, indices = noisy_logits.topk(self.top_k, dim=-1)
zeros = torch.full_like(noisy_logits, float('-inf'))
sparse_logits = zeros.scatter(-1, indices, top_k_logits)
router_output = F.softmax(sparse_logits, dim=-1)
return router_output, indices
讓我們再測試一下這個實現
#Testing this out, again:
num_experts = 8
top_k = 2
n_embd = 16
mh_output = torch.randn(2, 4, n_embd) # Example input
noisy_top_k_gate = NoisyTopkRouter(n_embd, num_experts, top_k)
gating_output, indices = noisy_top_k_gate(mh_output)
gating_output.shape, gating_output, indices
#It works!!
#output
(torch.Size([2, 4, 8]),
tensor([[[0.4181, 0.0000, 0.5819, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.4693, 0.5307, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.4985, 0.5015, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.2641, 0.0000, 0.7359, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, 0.6301, 0.0000, 0.3699, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.4766, 0.0000, 0.0000, 0.0000, 0.5234],
[0.0000, 0.0000, 0.0000, 0.6815, 0.0000, 0.0000, 0.3185, 0.0000],
[0.4482, 0.5518, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]],
grad_fn=<SoftmaxBackward0>),
tensor([[[2, 0],
[1, 0],
[2, 1],
[5, 3]],
[[3, 5],
[7, 3],
[3, 6],
[1, 0]]]))
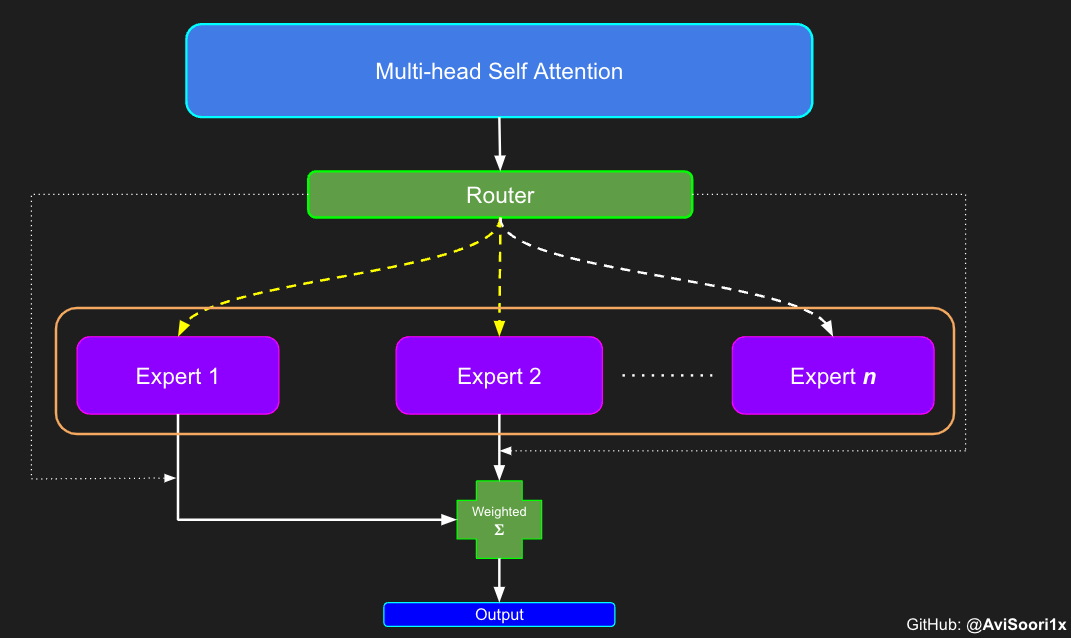
建立一個稀疏專家混合模組
此過程的主要方面涉及門控網路的輸出。在獲得這些結果後,將 top k 值與給定 token 的相應 top-k 專家輸出進行選擇性相乘。這種選擇性相乘形成一個加權和,構成 SparseMoe 塊的輸出。此過程的關鍵和挑戰部分是避免不必要的乘法。必須僅對 top_k 專家進行前向傳播,然後計算此加權和。對每個專家進行前向傳播將違背使用稀疏 MoE 的目的,因為它將不再是稀疏的。
class SparseMoE(nn.Module):
def __init__(self, n_embed, num_experts, top_k):
super(SparseMoE, self).__init__()
self.router = NoisyTopkRouter(n_embed, num_experts, top_k)
self.experts = nn.ModuleList([Expert(n_embed) for _ in range(num_experts)])
self.top_k = top_k
def forward(self, x):
gating_output, indices = self.router(x)
final_output = torch.zeros_like(x)
# Reshape inputs for batch processing
flat_x = x.view(-1, x.size(-1))
flat_gating_output = gating_output.view(-1, gating_output.size(-1))
# Process each expert in parallel
for i, expert in enumerate(self.experts):
# Create a mask for the inputs where the current expert is in top-k
expert_mask = (indices == i).any(dim=-1)
flat_mask = expert_mask.view(-1)
if flat_mask.any():
expert_input = flat_x[flat_mask]
expert_output = expert(expert_input)
# Extract and apply gating scores
gating_scores = flat_gating_output[flat_mask, i].unsqueeze(1)
weighted_output = expert_output * gating_scores
# Update final output additively by indexing and adding
final_output[expert_mask] += weighted_output.squeeze(1)
return final_output
使用示例輸入測試上述實現是否有效很有幫助。執行以下程式碼後,我們可以看到它確實有效!
import torch
import torch.nn as nn
#Let's test this out
num_experts = 8
top_k = 2
n_embd = 16
dropout=0.1
mh_output = torch.randn(4, 8, n_embd) # Example multi-head attention output
sparse_moe = SparseMoE(n_embd, num_experts, top_k)
final_output = sparse_moe(mh_output)
print("Shape of the final output:", final_output.shape)
Shape of the final output: torch.Size([4, 8, 16])
需要強調的是,重要的是要認識到,如上圖所示,來自路由器/門控網路的 top_k 專家輸出的幅值也至關重要。這些 top_k 索引標識了被啟用的專家,而這些 top_k 維度中值的幅值決定了它們各自的權重。加權求和的概念在下圖中得到了進一步強調。
將所有內容整合在一起
多頭自注意力和稀疏專家混合被組合起來,形成一個稀疏專家混合 Transformer 塊。就像在普通 Transformer 塊中一樣,添加了跳躍連線以確保訓練穩定並避免梯度消失等問題。此外,還採用了層歸一化來進一步穩定學習過程。
#Create a self attention + mixture of experts block, that may be repeated several number of times
class Block(nn.Module):
""" Mixture of Experts Transformer block: communication followed by computation (multi-head self attention + SparseMoE) """
def __init__(self, n_embed, n_head, num_experts, top_k):
# n_embed: embedding dimension, n_head: the number of heads we'd like
super().__init__()
head_size = n_embed // n_head
self.sa = MultiHeadAttention(n_head, head_size)
self.smoe = SparseMoE(n_embed, num_experts, top_k)
self.ln1 = nn.LayerNorm(n_embed)
self.ln2 = nn.LayerNorm(n_embed)
def forward(self, x):
x = x + self.sa(self.ln1(x))
x = x + self.smoe(self.ln2(x))
return x
最後,將所有內容整合在一起,以建立一個稀疏專家混合語言模型。
class SparseMoELanguageModel(nn.Module):
def __init__(self):
super().__init__()
# each token directly reads off the logits for the next token from a lookup table
self.token_embedding_table = nn.Embedding(vocab_size, n_embed)
self.position_embedding_table = nn.Embedding(block_size, n_embed)
self.blocks = nn.Sequential(*[Block(n_embed, n_head=n_head, num_experts=num_experts,top_k=top_k) for _ in range(n_layer)])
self.ln_f = nn.LayerNorm(n_embed) # final layer norm
self.lm_head = nn.Linear(n_embed, vocab_size)
def forward(self, idx, targets=None):
B, T = idx.shape
# idx and targets are both (B,T) tensor of integers
tok_emb = self.token_embedding_table(idx) # (B,T,C)
pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)
x = tok_emb + pos_emb # (B,T,C)
x = self.blocks(x) # (B,T,C)
x = self.ln_f(x) # (B,T,C)
logits = self.lm_head(x) # (B,T,vocab_size)
if targets is None:
loss = None
else:
B, T, C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss
def generate(self, idx, max_new_tokens):
# idx is (B, T) array of indices in the current context
for _ in range(max_new_tokens):
# crop idx to the last block_size tokens
idx_cond = idx[:, -block_size:]
# get the predictions
logits, loss = self(idx_cond)
# focus only on the last time step
logits = logits[:, -1, :] # becomes (B, C)
# apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # (B, C)
# sample from the distribution
idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
# append sampled index to the running sequence
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idx
初始化對於深度神經網路的高效訓練至關重要。此處使用 Kaiming He 初始化是因為專家中存在 ReLU 啟用。歡迎嘗試 Glorot 初始化,它在 Transformer 中更常用。Jeremy Howard 的 Fastai Part 2 有一節出色的講座,從頭開始實現了這些內容:https://course.fast.ai/Lessons/lesson17.html。文獻中指出 Glorot 初始化通常用於 Transformer 模型,因此這是一個可能改善模型效能的機會。
def kaiming_init_weights(m):
if isinstance (m, (nn.Linear)):
init.kaiming_normal_(m.weight)
model = SparseMoELanguageModel()
model.apply(kaiming_init_weights)
我使用 mlflow 來跟蹤和記錄重要的指標以及訓練超引數。我在這裡展示的訓練迴圈包含了這些程式碼。如果您只想在不使用 mlflow 的情況下進行訓練,makeMoE github 倉庫中的 notebook 包含不帶 MLFlow 的程式碼塊。我個人覺得跟蹤引數和指標非常方便,尤其是在進行實驗時。
#Using MLFlow
m = model.to(device)
# print the number of parameters in the model
print(sum(p.numel() for p in m.parameters())/1e6, 'M parameters')
# create a PyTorch optimizer
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)
#mlflow.set_experiment("makeMoE")
with mlflow.start_run():
#If you use mlflow.autolog() this will be automatically logged. I chose to explicitly log here for completeness
params = {"batch_size": batch_size , "block_size" : block_size, "max_iters": max_iters, "eval_interval": eval_interval,
"learning_rate": learning_rate, "device": device, "eval_iters": eval_iters, "dropout" : dropout, "num_experts": num_experts, "top_k": top_k }
mlflow.log_params(params)
for iter in range(max_iters):
# every once in a while evaluate the loss on train and val sets
if iter % eval_interval == 0 or iter == max_iters - 1:
losses = estimate_loss()
print(f"step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")
metrics = {"train_loss": losses['train'], "val_loss": losses['val']}
mlflow.log_metrics(metrics, step=iter)
# sample a batch of data
xb, yb = get_batch('train')
# evaluate the loss
logits, loss = model(xb, yb)
optimizer.zero_grad(set_to_none=True)
loss.backward()
optimizer.step()
8.996545 M parameters
step 0: train loss 5.3223, val loss 5.3166
step 100: train loss 2.7351, val loss 2.7429
step 200: train loss 2.5125, val loss 2.5233
.
.
.
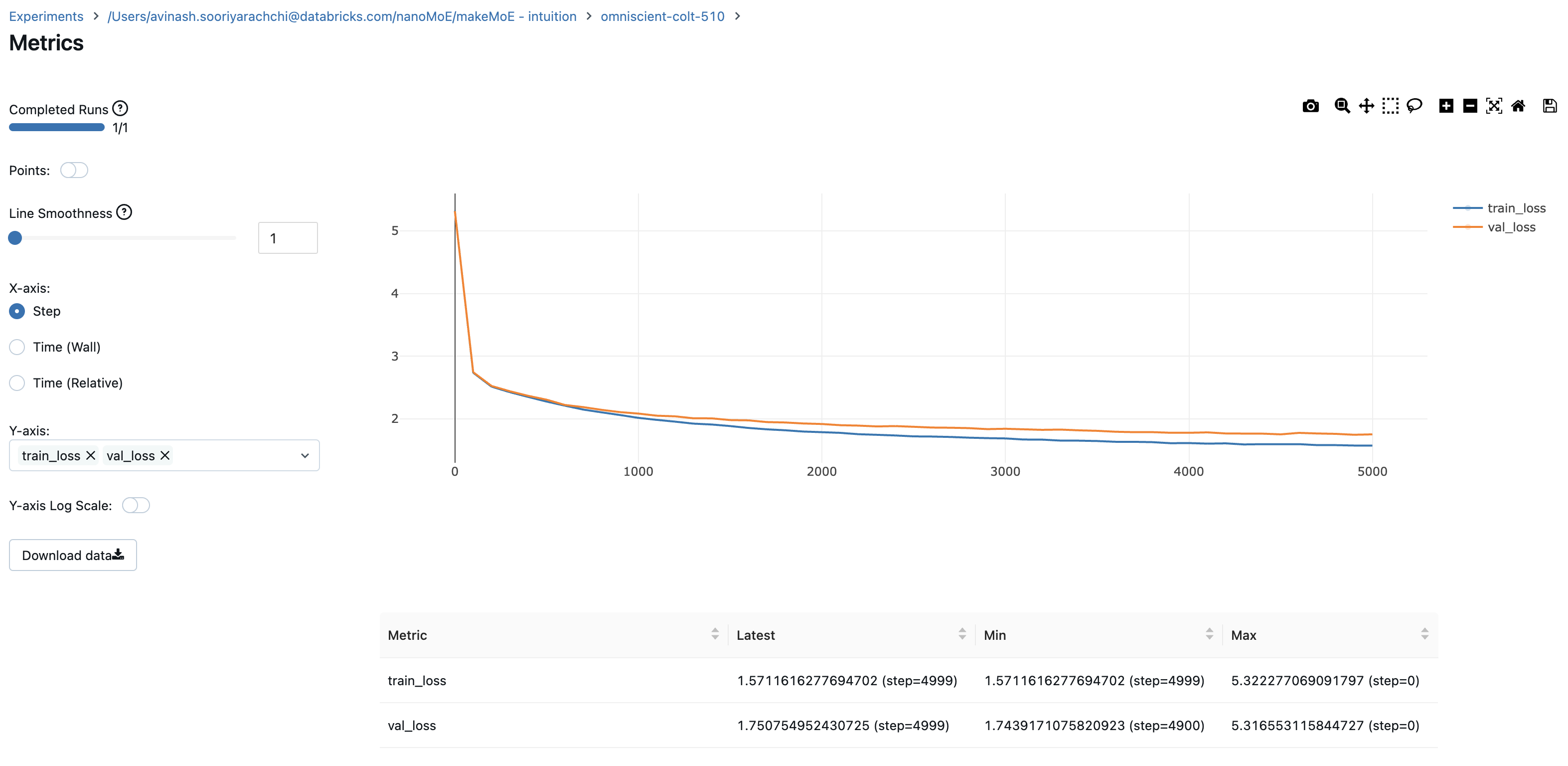
step 4999: train loss 1.5712, val loss 1.7508
記錄訓練和驗證損失可以很好地指示訓練進展。該圖顯示我可能應該在 4500 步左右停止(當時驗證損失略有上升)。
現在我們可以使用這個模型逐個字元地自迴歸地生成文字。對於一個稀疏啟用的約 900 萬引數模型,我沒有什麼可抱怨的。
# generate from the model. Not great. Not too bad either
context = torch.zeros((1, 1), dtype=torch.long, device=device)
print(decode(m.generate(context, max_new_tokens=2000)[0].tolist()))
DUKE VINCENVENTIO:
If it ever fecond he town sue kigh now,
That thou wold'st is steen 't.
SIMNA:
Angent her; no, my a born Yorthort,
Romeoos soun and lawf to your sawe with ch a woft ttastly defy,
To declay the soul art; and meart smad.
CORPIOLLANUS:
Which I cannot shall do from by born und ot cold warrike,
What king we best anone wrave's going of heard and good
Thus playvage; you have wold the grace.
...
我希望這個解釋能幫助您理解稀疏專家混合模型架構及其工作原理。
我在這項實現中大量參考了以下出版物:
- Mixtral of experts: https://arxiv.org/pdf/2401.04088.pdf
- Outrageously Large Neural Networks: The Sparsely-Gated Mixture-Of-Experts layer: https://arxiv.org/pdf/1701.06538.pdf
Andrej Karpathy 的原始 makemore 實現
該程式碼完全在 Databricks 上使用單個 A100 GPU 開發。如果您在 Databricks 上執行此程式碼,您可以在您選擇的雲提供商上將它擴充套件到任意大的 GPU 叢集,沒有任何問題。我選擇使用 MLFlow(Databricks 中預裝了它。它是完全開源的,您可以在其他地方輕鬆地透過 pip 安裝),因為我發現它有助於跟蹤和記錄所有必要的指標。這完全是可選的。請注意,該實現強調可讀性和可修改性而不是效能,因此您可以透過多種方式改進它。
鑑於此,這裡有一些你可以嘗試的事情:
- 使專家混合模組更高效。我相信在上述實現中,對於正確專家的稀疏啟用可以進行顯著改進。
- 嘗試不同的神經網路初始化策略。我列出的來源(Fastai 第二部分)非常棒。
- 從字元級到子詞分詞
- 對專家數量和 top_k(每個 token 啟用的專家數量)進行貝葉斯超引數搜尋。這可以粗略地歸類為神經網路架構搜尋。
- 此處未討論或實現專家容量。這絕對值得探索。
鑑於人們對專家混合和多模態的興趣,觀察兩者交叉領域的發展也將非常有趣。祝您玩得開心!!
PS:本部落格的第二部分,包含更高效訓練的專家容量實現,請參見此處:https://huggingface.co/blog/AviSoori1x/makemoe2