註解擴散模型

釋出於 2022 年 6 月 7 日

在 GitHub 上更新

贊

254

在這篇部落格文章中，我們將深入探討**去噪擴散機率模型**（也稱為 DDPM、擴散模型、基於分數的生成模型或簡稱自編碼器），因為研究人員已透過它們在（有）條件影像/音訊/影片生成方面取得了卓越的成果。目前（撰寫本文時）流行的例子包括 OpenAI 的GLIDE和DALL-E 2，海德堡大學的Latent Diffusion和 Google Brain 的ImageGen。

我們將回顧 (Ho 等人，2020) 的原始 DDPM 論文，並根據 Phil Wang 的實現（該實現本身基於原始 TensorFlow 實現）在 PyTorch 中逐步實現它。請注意，用於生成建模的擴散思想實際上在 (Sohl-Dickstein 等人，2015) 中已經提出。然而，直到 (Song 等人，2019)（斯坦福大學）和隨後的 (Ho 等人，2020)（Google Brain）獨立改進了該方法。

請注意，擴散模型有多種視角。這裡，我們採用離散時間（潛在變數模型）的視角，但請務必也檢視其他視角。

好的，讓我們開始吧！

from IPython.display import Image
Image(filename='assets/78_annotated-diffusion/ddpm_paper.png')

我們首先安裝並匯入所需的庫（假設您已安裝 PyTorch）。

!pip install -q -U einops datasets matplotlib tqdm

import math
from inspect import isfunction
from functools import partial

%matplotlib inline
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
from einops import rearrange, reduce
from einops.layers.torch import Rearrange

import torch
from torch import nn, einsum
import torch.nn.functional as F

什麼是擴散模型？

去噪擴散模型與其他生成模型（如歸一化流、GAN 或 VAE）相比並不復雜：它們都將來自某個簡單分佈的噪聲轉換為資料樣本。這裡也是如此，**神經網路學習從純噪聲開始逐漸去噪資料**。

更具體地針對影像，該設定包含 2 個過程：

我們選擇的固定（或預定義）正向擴散過程 $q$ ，它逐漸向影像新增高斯噪聲，直到最終變為純噪聲
一個學習到的反向去噪擴散過程 $p_\theta$ ，其中訓練神經網路從純噪聲開始逐漸去噪影像，直到最終得到真實影像。

正向和反向過程都由 $t$ 索引，在有限的時間步長 $T$ 內進行（DDPM 作者使用 $T=1000$ ）。您從 $t=0$ 開始，從資料分佈中取樣真實影像 $\mathbf{x}_0$ （例如 ImageNet 中的貓影像），並且正向過程在每個時間步長 $t$ 從高斯分佈中取樣一些噪聲，並將其新增到上一個時間步長的影像中。給定足夠大的 $T$ 和在每個時間步長新增噪聲的良好排程，您最終將在 $t=T$ 處透過漸進過程得到所謂的各向同性高斯分佈。

更數學化的形式

讓我們更正式地寫下來，因為最終我們需要一個可處理的損失函式，我們的神經網路需要對其進行最佳化。

令 $q(\mathbf{x}_0)$ 為真實資料分佈，例如“真實影像”。我們可以從這個分佈中取樣得到影像， $\mathbf{x}_0 \sim q(\mathbf{x}_0)$ 。我們定義正向擴散過程 $q(\mathbf{x}_t | \mathbf{x}_{t-1})$ ，它在每個時間步長 $t$ 根據已知方差排程 $0 < \beta_1 < \beta_2 < ... < \beta_T < 1$ 新增高斯噪聲，如下所示： $q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}).$

回想一下，正態分佈（也稱為高斯分佈）由兩個引數定義：均值 $\mu$ 和方差 $\sigma^2 \geq 0$ 。基本上，每個在時間步長 $t$ 處的新（略微嘈雜的）影像都從**條件高斯分佈**中抽取，其均值為 $\mathbf{\mu}_t = \sqrt{1 - \beta_t} \mathbf{x}_{t-1}$ ，方差為 $\sigma^2_t = \beta_t$ ，我們可以透過取樣 $\mathbf{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ ，然後設定 $\mathbf{x}_t = \sqrt{1 - \beta_t} \mathbf{x}_{t-1} + \sqrt{\beta_t} \mathbf{\epsilon}$ 。

請注意， $\beta_t$ 在每個時間步長 $t$ 並不恆定（因此帶有下標）——實際上，我們定義了一個所謂的**“方差排程”**，它可以是線性的、二次的、餘弦的等等，我們將在後面看到（有點像學習率排程）。

所以從 $\mathbf{x}_0$ 開始，我們最終得到 $\mathbf{x}_1, ..., \mathbf{x}_t, ..., \mathbf{x}_T$ ，如果我們將排程設定得當，其中 $\mathbf{x}_T$ 是純高斯噪聲。

現在，如果知道條件分佈 $p(\mathbf{x}_{t-1} | \mathbf{x}_t)$ ，那麼就可以反向執行該過程：透過取樣一些隨機高斯噪聲 $\mathbf{x}_T$ ，然後逐漸“去噪”，最終得到從真實分佈 $\mathbf{x}_0$ 中取樣的樣本。

但是，我們不知道 $p(\mathbf{x}_{t-1} | \mathbf{x}_t)$ 。由於它需要知道所有可能影像的分佈才能計算這個條件機率，因此它是難以處理的。因此，我們將利用神經網路來**近似（學習）這個條件機率分佈**，我們稱之為 $p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_t)$ ，其中 $\theta$ 是神經網路的引數，透過梯度下降更新。

好的，所以我們需要一個神經網路來表示反向過程的（條件）機率分佈。如果我們假設這個反向過程也是高斯分佈，那麼回想一下，任何高斯分佈都由兩個引數定義：

一個由 $\mu_\theta$ 引數化的均值；
一個由 $\Sigma_\theta$ 引數化的方差；

因此，我們可以將該過程引數化為 $p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_{t},t), \Sigma_\theta (\mathbf{x}_{t},t))$ ，其中均值和方差也取決於噪聲水平 $t$ 。

因此，我們的神經網路需要學習/表示均值和方差。然而，DDPM 作者決定**固定方差，並讓神經網路只學習（表示）這個條件機率分佈的均值 $\mu_\theta$ **。論文中提到：

首先，我們將 $\Sigma_\theta ( \mathbf{x}_t, t) = \sigma^2_t \mathbf{I}$ 為未訓練的時間相關常數。實驗表明， $\sigma^2_t = \beta_t$ 和 $\sigma^2_t = \tilde{\beta}_t$ （見論文）取得了相似的結果。

這後來在改進擴散模型論文中得到了改進，除了均值之外，神經網路還學習這個反向過程的方差。

所以我們繼續，假設我們的神經網路只需要學習/表示這個條件機率分佈的均值。

定義目標函式（透過重新引數化均值）

為了推匯出學習反向過程均值的目標函式，作者觀察到 $q$ 和 $p_\theta$ 的組合可以看作是一個變分自編碼器（VAE）(Kingma 等人，2013)。因此，**變分下界**（也稱為 ELBO）可以用於最小化相對於真實資料樣本 $\mathbf{x}_0$ 的負對數似然（我們參考 VAE 論文了解 ELBO 的詳細資訊）。結果表明，這個過程的 ELBO 是每個時間步長 $t$ 的損失之和，即 $L = L_0 + L_1 + ... + L_T$ 。透過構建正向 $q$ 過程和反向過程，損失的每一項（除了 $L_0$ ）實際上都是**兩個高斯分佈之間的 KL 散度**，它可以明確地寫成關於均值的 L2 損失！

正如 Sohl-Dickstein 等人所示，所構建的正向過程 $q$ 的直接結果是，我們可以在任何任意噪聲水平下根據 $\mathbf{x}_0$ 取樣 $\mathbf{x}_t$ （因為高斯分佈之和也是高斯分佈）。這非常方便：我們不需要重複應用 $q$ 來取樣 $\mathbf{x}_t$ 。我們有 $q(\mathbf{x}_t | \mathbf{x}_0) = \cal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1- \bar{\alpha}_t) \mathbf{I})$

其中 $\alpha_t := 1 - \beta_t$ 和 $\bar{\alpha}_t := \Pi_{s=1}^{t} \alpha_s$ 。我們將此方程稱為“良好性質”。這意味著我們可以對高斯噪聲進行取樣並進行適當縮放，然後將其新增到 $\mathbf{x}_0$ 以直接得到 $\mathbf{x}_t$ 。請注意， $\bar{\alpha}_t$ 是已知 $\beta_t$ 方差排程函式的函式，因此也是已知的，可以預先計算。這使得我們能夠在訓練期間最佳化損失函式 $L$ 的隨機項（換句話說，在訓練期間隨機取樣 $t$ 並最佳化 $L_t$ ）。

這個性質的另一個優點是，正如Ho等人所示，可以（經過一些數學推導，我們在此將讀者指向這篇優秀部落格文章）重新引數化均值，使神經網路學習（預測）新增的噪聲（透過網路 $\mathbf{\epsilon}_\theta(\mathbf{x}_t, t)$ ）用於構成損失的KL項中的噪聲水平 $t$ 。這意味著我們的神經網路將成為噪聲預測器，而不是（直接的）均值預測器。均值可以計算如下：

$\mathbf{\mu}_\theta(\mathbf{x}_t, t) = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1- \bar{\alpha}_t}} \mathbf{\epsilon}_\theta(\mathbf{x}_t, t) \right)$

最終的目標函式 $L_t$ 如下所示（對於給定 $\mathbf{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ 的隨機時間步 $t$ ）

$\| \mathbf{\epsilon} - \mathbf{\epsilon}_\theta(\mathbf{x}_t, t) \|^2 = \| \mathbf{\epsilon} - \mathbf{\epsilon}_\theta( \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{(1- \bar{\alpha}_t) } \mathbf{\epsilon}, t) \|^2.$

這裡， $\mathbf{x}_0$ 是初始（真實，未損壞的）影像，我們看到由固定正向過程給出的直接噪聲水平 $t$ 樣本。 $\mathbf{\epsilon}$ 是在時間步 $t$ 取樣的純噪聲，而 $\mathbf{\epsilon}_\theta (\mathbf{x}_t, t)$ 是我們的神經網路。神經網路透過真實噪聲和預測高斯噪聲之間的簡單均方誤差 (MSE) 進行最佳化。

訓練演算法現在看起來如下：

換句話說，

我們從真實的未知且可能複雜的資料分佈 $q(\mathbf{x}_0)$ 中隨機取樣一個樣本 $\mathbf{x}_0$
我們從1到 $T$ 均勻取樣一個噪聲水平 $t$ （即隨機時間步）
我們從高斯分佈中取樣一些噪聲，並使用該噪聲在水平 $t$ 處損壞輸入（使用上面定義的良好性質）
神經網路經過訓練，根據損壞的影像 $\mathbf{x}_t$ （即根據已知排程 $\beta_t$ 應用於 $\mathbf{x}_0$ 的噪聲）來預測此噪聲

實際上，所有這些都是在資料批次上完成的，因為我們使用隨機梯度下降來最佳化神經網路。

神經網路

神經網路需要接受在特定時間步被加噪的影像，並返回預測的噪聲。請注意，預測的噪聲是一個與輸入影像具有相同大小/解析度的張量。所以從技術上講，網路輸入和輸出形狀相同的張量。我們可以為此使用哪種型別的神經網路呢？

這裡通常使用的是與自編碼器非常相似的架構，你可能在典型的“深度學習入門”教程中記得它。自編碼器在編碼器和解碼器之間有一個所謂的“瓶頸”層。編碼器首先將影像編碼為較小的隱藏表示，稱為“瓶頸”，然後解碼器將該隱藏表示解碼回實際影像。這迫使網路只在瓶頸層中保留最重要的資訊。

在架構方面，DDPM 作者選擇了 **U-Net**，由（Ronneberger 等人，2015）引入（當時在醫學影像分割領域取得了最先進的成果）。這個網路，像任何自編碼器一樣，中間包含一個瓶頸，確保網路只學習最重要的資訊。重要的是，它在編碼器和解碼器之間引入了殘差連線，極大地改善了梯度流（受 He 等人，2015 的 ResNet 啟發）。

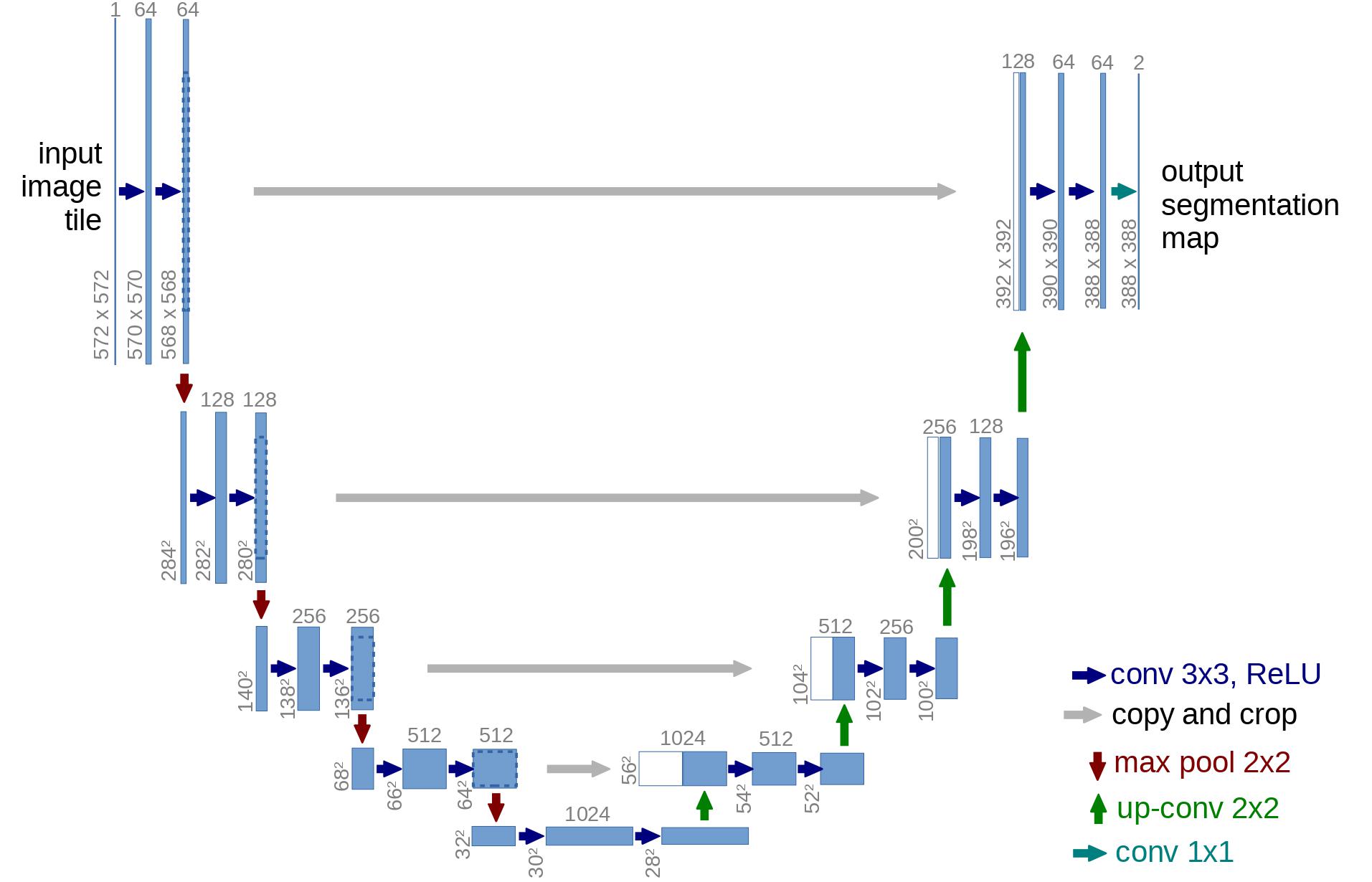
可以看出，U-Net 模型首先對輸入進行下采樣（即在空間解析度方面使輸入變小），然後執行上取樣。

下面，我們將逐步實現這個網路。

網路輔助函式

首先，我們定義一些輔助函式和類，它們將在實現神經網路時使用。重要的是，我們定義了一個`Residual`模組，它簡單地將輸入新增到特定函式的輸出中（換句話說，為特定函式添加了一個殘差連線）。

我們還為上取樣和下采樣操作定義了別名。

def exists(x):
    return x is not None

def default(val, d):
    if exists(val):
        return val
    return d() if isfunction(d) else d


def num_to_groups(num, divisor):
    groups = num // divisor
    remainder = num % divisor
    arr = [divisor] * groups
    if remainder > 0:
        arr.append(remainder)
    return arr


class Residual(nn.Module):
    def __init__(self, fn):
        super().__init__()
        self.fn = fn

    def forward(self, x, *args, **kwargs):
        return self.fn(x, *args, **kwargs) + x


def Upsample(dim, dim_out=None):
    return nn.Sequential(
        nn.Upsample(scale_factor=2, mode="nearest"),
        nn.Conv2d(dim, default(dim_out, dim), 3, padding=1),
    )


def Downsample(dim, dim_out=None):
    # No More Strided Convolutions or Pooling
    return nn.Sequential(
        Rearrange("b c (h p1) (w p2) -> b (c p1 p2) h w", p1=2, p2=2),
        nn.Conv2d(dim * 4, default(dim_out, dim), 1),
    )

位置嵌入

由於神經網路的引數在時間（噪聲水平）上是共享的，因此作者採用正弦位置嵌入來編碼 $t$ ，這受到了Transformer（Vaswani et al., 2017）的啟發。這使得神經網路“知道”它在批處理中的每個影像都在哪個特定時間步（噪聲水平）下執行。

SinusoidalPositionEmbeddings模組將形狀為`(batch_size, 1)`的張量作為輸入（即批處理中幾個嘈雜影像的噪聲水平），並將其轉換為形狀為`(batch_size, dim)`的張量，其中`dim`是位置嵌入的維度。然後將其新增到每個殘差塊中，我們將在後面看到。

class SinusoidalPositionEmbeddings(nn.Module):
    def __init__(self, dim):
        super().__init__()
        self.dim = dim

    def forward(self, time):
        device = time.device
        half_dim = self.dim // 2
        embeddings = math.log(10000) / (half_dim - 1)
        embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
        embeddings = time[:, None] * embeddings[None, :]
        embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
        return embeddings

ResNet 塊

接下來，我們定義 U-Net 模型的核心構建塊。DDPM 作者採用了 Wide ResNet 塊（Zagoruyko 等人，2016），但 Phil Wang 將標準卷積層替換為“權重標準化”版本，這與組歸一化結合使用效果更好（詳見（Kolesnikov 等人，2019））。

class WeightStandardizedConv2d(nn.Conv2d):
    """
    https://arxiv.org/abs/1903.10520
    weight standardization purportedly works synergistically with group normalization
    """

    def forward(self, x):
        eps = 1e-5 if x.dtype == torch.float32 else 1e-3

        weight = self.weight
        mean = reduce(weight, "o ... -> o 1 1 1", "mean")
        var = reduce(weight, "o ... -> o 1 1 1", partial(torch.var, unbiased=False))
        normalized_weight = (weight - mean) * (var + eps).rsqrt()

        return F.conv2d(
            x,
            normalized_weight,
            self.bias,
            self.stride,
            self.padding,
            self.dilation,
            self.groups,
        )


class Block(nn.Module):
    def __init__(self, dim, dim_out, groups=8):
        super().__init__()
        self.proj = WeightStandardizedConv2d(dim, dim_out, 3, padding=1)
        self.norm = nn.GroupNorm(groups, dim_out)
        self.act = nn.SiLU()

    def forward(self, x, scale_shift=None):
        x = self.proj(x)
        x = self.norm(x)

        if exists(scale_shift):
            scale, shift = scale_shift
            x = x * (scale + 1) + shift

        x = self.act(x)
        return x


class ResnetBlock(nn.Module):
    """https://arxiv.org/abs/1512.03385"""

    def __init__(self, dim, dim_out, *, time_emb_dim=None, groups=8):
        super().__init__()
        self.mlp = (
            nn.Sequential(nn.SiLU(), nn.Linear(time_emb_dim, dim_out * 2))
            if exists(time_emb_dim)
            else None
        )

        self.block1 = Block(dim, dim_out, groups=groups)
        self.block2 = Block(dim_out, dim_out, groups=groups)
        self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity()

    def forward(self, x, time_emb=None):
        scale_shift = None
        if exists(self.mlp) and exists(time_emb):
            time_emb = self.mlp(time_emb)
            time_emb = rearrange(time_emb, "b c -> b c 1 1")
            scale_shift = time_emb.chunk(2, dim=1)

        h = self.block1(x, scale_shift=scale_shift)
        h = self.block2(h)
        return h + self.res_conv(x)

注意力模組

接下來，我們定義注意力模組，DDPM 的作者將其新增在卷積塊之間。注意力是著名的 Transformer 架構（Vaswani et al., 2017）的基本組成部分，該架構在 AI 的各個領域都取得了巨大成功，從自然語言處理和視覺到蛋白質摺疊。Phil Wang 採用了兩種注意力變體：一種是常規的多頭自注意力（如 Transformer 中使用的），另一種是線性注意力變體（Shen et al., 2018），其時間和記憶體需求隨序列長度線性縮放，而常規注意力是二次方縮放。

有關注意力機制的詳細解釋，請參閱 Jay Allamar 的精彩部落格文章。

class Attention(nn.Module):
    def __init__(self, dim, heads=4, dim_head=32):
        super().__init__()
        self.scale = dim_head**-0.5
        self.heads = heads
        hidden_dim = dim_head * heads
        self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
        self.to_out = nn.Conv2d(hidden_dim, dim, 1)

    def forward(self, x):
        b, c, h, w = x.shape
        qkv = self.to_qkv(x).chunk(3, dim=1)
        q, k, v = map(
            lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
        )
        q = q * self.scale

        sim = einsum("b h d i, b h d j -> b h i j", q, k)
        sim = sim - sim.amax(dim=-1, keepdim=True).detach()
        attn = sim.softmax(dim=-1)

        out = einsum("b h i j, b h d j -> b h i d", attn, v)
        out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)
        return self.to_out(out)

class LinearAttention(nn.Module):
    def __init__(self, dim, heads=4, dim_head=32):
        super().__init__()
        self.scale = dim_head**-0.5
        self.heads = heads
        hidden_dim = dim_head * heads
        self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)

        self.to_out = nn.Sequential(nn.Conv2d(hidden_dim, dim, 1), 
                                    nn.GroupNorm(1, dim))

    def forward(self, x):
        b, c, h, w = x.shape
        qkv = self.to_qkv(x).chunk(3, dim=1)
        q, k, v = map(
            lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
        )

        q = q.softmax(dim=-2)
        k = k.softmax(dim=-1)

        q = q * self.scale
        context = torch.einsum("b h d n, b h e n -> b h d e", k, v)

        out = torch.einsum("b h d e, b h d n -> b h e n", context, q)
        out = rearrange(out, "b h c (x y) -> b (h c) x y", h=self.heads, x=h, y=w)
        return self.to_out(out)

組歸一化

DDPM 的作者將 U-Net 的卷積層/注意力層與組歸一化（Wu et al., 2018）交織在一起。下面，我們定義了一個 `PreNorm` 類，它將用於在注意力層之前應用組歸一化，我們將在後面看到。請注意，關於在 Transformer 中是在注意力之前還是之後應用歸一化，一直存在爭議。

class PreNorm(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.fn = fn
        self.norm = nn.GroupNorm(1, dim)

    def forward(self, x):
        x = self.norm(x)
        return self.fn(x)

條件 U-Net

現在我們已經定義了所有構建塊（位置嵌入、ResNet 塊、注意力和組歸一化），是時候定義整個神經網路了。回想一下，網路 $\mathbf{\epsilon}_\theta(\mathbf{x}_t, t)$ 的工作是接收一批帶噪聲的影像及其各自的噪聲水平，並輸出新增到輸入中的噪聲。更正式地說：

網路接收一批形狀為`(batch_size, num_channels, height, width)`的噪聲影像和一批形狀為`(batch_size, 1)`的噪聲水平作為輸入，並返回形狀為`(batch_size, num_channels, height, width)`的張量

網路構建如下：

首先，對一批帶噪聲的影像應用卷積層，併為噪聲水平計算位置嵌入。
接下來，應用一系列下采樣階段。每個下采樣階段由2個ResNet塊+組歸一化+注意力+殘差連線+一個下采樣操作組成。
在網路的中間，再次應用ResNet塊，並穿插注意力。
接下來，應用一系列上取樣階段。每個上取樣階段由2個ResNet塊+組歸一化+注意力+殘差連線+一個上取樣操作組成。
最後，應用一個ResNet塊，然後是一個卷積層。

最終，神經網路就像樂高積木一樣堆疊層（但理解它們的工作原理很重要）。

class Unet(nn.Module):
    def __init__(
        self,
        dim,
        init_dim=None,
        out_dim=None,
        dim_mults=(1, 2, 4, 8),
        channels=3,
        self_condition=False,
        resnet_block_groups=4,
    ):
        super().__init__()

        # determine dimensions
        self.channels = channels
        self.self_condition = self_condition
        input_channels = channels * (2 if self_condition else 1)

        init_dim = default(init_dim, dim)
        self.init_conv = nn.Conv2d(input_channels, init_dim, 1, padding=0) # changed to 1 and 0 from 7,3

        dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
        in_out = list(zip(dims[:-1], dims[1:]))

        block_klass = partial(ResnetBlock, groups=resnet_block_groups)

        # time embeddings
        time_dim = dim * 4

        self.time_mlp = nn.Sequential(
            SinusoidalPositionEmbeddings(dim),
            nn.Linear(dim, time_dim),
            nn.GELU(),
            nn.Linear(time_dim, time_dim),
        )

        # layers
        self.downs = nn.ModuleList([])
        self.ups = nn.ModuleList([])
        num_resolutions = len(in_out)

        for ind, (dim_in, dim_out) in enumerate(in_out):
            is_last = ind >= (num_resolutions - 1)

            self.downs.append(
                nn.ModuleList(
                    [
                        block_klass(dim_in, dim_in, time_emb_dim=time_dim),
                        block_klass(dim_in, dim_in, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_in, LinearAttention(dim_in))),
                        Downsample(dim_in, dim_out)
                        if not is_last
                        else nn.Conv2d(dim_in, dim_out, 3, padding=1),
                    ]
                )
            )

        mid_dim = dims[-1]
        self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
        self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
        self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)

        for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):
            is_last = ind == (len(in_out) - 1)

            self.ups.append(
                nn.ModuleList(
                    [
                        block_klass(dim_out + dim_in, dim_out, time_emb_dim=time_dim),
                        block_klass(dim_out + dim_in, dim_out, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_out, LinearAttention(dim_out))),
                        Upsample(dim_out, dim_in)
                        if not is_last
                        else nn.Conv2d(dim_out, dim_in, 3, padding=1),
                    ]
                )
            )

        self.out_dim = default(out_dim, channels)

        self.final_res_block = block_klass(dim * 2, dim, time_emb_dim=time_dim)
        self.final_conv = nn.Conv2d(dim, self.out_dim, 1)

    def forward(self, x, time, x_self_cond=None):
        if self.self_condition:
            x_self_cond = default(x_self_cond, lambda: torch.zeros_like(x))
            x = torch.cat((x_self_cond, x), dim=1)

        x = self.init_conv(x)
        r = x.clone()

        t = self.time_mlp(time)

        h = []

        for block1, block2, attn, downsample in self.downs:
            x = block1(x, t)
            h.append(x)

            x = block2(x, t)
            x = attn(x)
            h.append(x)

            x = downsample(x)

        x = self.mid_block1(x, t)
        x = self.mid_attn(x)
        x = self.mid_block2(x, t)

        for block1, block2, attn, upsample in self.ups:
            x = torch.cat((x, h.pop()), dim=1)
            x = block1(x, t)

            x = torch.cat((x, h.pop()), dim=1)
            x = block2(x, t)
            x = attn(x)

            x = upsample(x)

        x = torch.cat((x, r), dim=1)

        x = self.final_res_block(x, t)
        return self.final_conv(x)

定義正向擴散過程

正向擴散過程在多個時間步 $T$ 中逐漸向真實分佈中的影像新增噪聲。這根據方差排程進行。最初的 DDPM 作者採用線性排程：

我們將正向過程方差設定為從 $\beta_1 = 10^{−4}$ 線性增加到 $\beta_T = 0.02$ 的常數。

然而，(Nichol et al., 2021) 的研究表明，採用餘弦排程可以取得更好的結果。

下面，我們定義了 $T$ 時間步的各種排程（我們稍後會選擇其中一個）。

def cosine_beta_schedule(timesteps, s=0.008):
    """
    cosine schedule as proposed in https://arxiv.org/abs/2102.09672
    """
    steps = timesteps + 1
    x = torch.linspace(0, timesteps, steps)
    alphas_cumprod = torch.cos(((x / timesteps) + s) / (1 + s) * torch.pi * 0.5) ** 2
    alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
    betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
    return torch.clip(betas, 0.0001, 0.9999)

def linear_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return torch.linspace(beta_start, beta_end, timesteps)

def quadratic_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return torch.linspace(beta_start**0.5, beta_end**0.5, timesteps) ** 2

def sigmoid_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    betas = torch.linspace(-6, 6, timesteps)
    return torch.sigmoid(betas) * (beta_end - beta_start) + beta_start

首先，讓我們使用 $T=300$ 個時間步的線性排程，並定義我們將需要的來自 $\beta_t$ 的各種變數，例如方差的累積乘積 $\bar{\alpha}_t$ 。下面的每個變數都只是一個一維張量，儲存從 $t$ 到 $T$ 的值。重要的是，我們還定義了一個`extract`函式，它允許我們為一批索引提取適當的 $t$ 索引。

timesteps = 300

# define beta schedule
betas = linear_beta_schedule(timesteps=timesteps)

# define alphas 
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)

# calculations for diffusion q(x_t | x_{t-1}) and others
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)

# calculations for posterior q(x_{t-1} | x_t, x_0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)

def extract(a, t, x_shape):
    batch_size = t.shape[0]
    out = a.gather(-1, t.cpu())
    return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)

我們將用貓的影像來說明在擴散過程的每個時間步如何新增噪聲。

from PIL import Image
import requests

url = 'http://images.cocodataset.org/val2017/000000039769.jpg'
image = Image.open(requests.get(url, stream=True).raw) # PIL image of shape HWC
image

噪聲被新增到 PyTorch 張量中，而不是 Pillow 影像中。我們首先定義影像轉換，允許我們從 PIL 影像轉換為 PyTorch 張量（我們可以在其上新增噪聲），反之亦然。

這些轉換相當簡單：我們首先將影像除以 $255$ 進行歸一化（使它們在 $[0,1]$ 範圍內），然後確保它們在 $[-1, 1]$ 範圍內。根據 DDPM 論文：

我們假設影像資料由 $\{0, 1, ... , 255\}$ 中的整陣列成，併線性縮放到 $[−1, 1]$ 。這確保了神經網路逆向過程在從標準正態先驗 $p(\mathbf{x}_T )$ 開始時，以一致縮放的輸入進行操作。

from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize

image_size = 128
transform = Compose([
    Resize(image_size),
    CenterCrop(image_size),
    ToTensor(), # turn into torch Tensor of shape CHW, divide by 255
    Lambda(lambda t: (t * 2) - 1),
    
])

x_start = transform(image).unsqueeze(0)
x_start.shape

Output:
----------------------------------------------------------------------------------------------------
torch.Size([1, 3, 128, 128])

我們還定義了反向轉換，它接受一個包含 $[-1, 1]$ 範圍內值的 PyTorch 張量，並將其轉換回 PIL 影像

import numpy as np

reverse_transform = Compose([
     Lambda(lambda t: (t + 1) / 2),
     Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC
     Lambda(lambda t: t * 255.),
     Lambda(lambda t: t.numpy().astype(np.uint8)),
     ToPILImage(),
])

讓我們驗證一下

reverse_transform(x_start.squeeze())

我們現在可以像論文中那樣定義正向擴散過程：

# forward diffusion (using the nice property)
def q_sample(x_start, t, noise=None):
    if noise is None:
        noise = torch.randn_like(x_start)

    sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
    sqrt_one_minus_alphas_cumprod_t = extract(
        sqrt_one_minus_alphas_cumprod, t, x_start.shape
    )

    return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise

讓我們在一個特定的時間步上測試它。

def get_noisy_image(x_start, t):
  # add noise
  x_noisy = q_sample(x_start, t=t)

  # turn back into PIL image
  noisy_image = reverse_transform(x_noisy.squeeze())

  return noisy_image

# take time step
t = torch.tensor([40])

get_noisy_image(x_start, t)

讓我們在不同的時間步視覺化這一點。

import matplotlib.pyplot as plt

# use seed for reproducability
torch.manual_seed(0)

# source: https://pytorch.org/vision/stable/auto_examples/plot_transforms.html#sphx-glr-auto-examples-plot-transforms-py
def plot(imgs, with_orig=False, row_title=None, **imshow_kwargs):
    if not isinstance(imgs[0], list):
        # Make a 2d grid even if there's just 1 row
        imgs = [imgs]

    num_rows = len(imgs)
    num_cols = len(imgs[0]) + with_orig
    fig, axs = plt.subplots(figsize=(200,200), nrows=num_rows, ncols=num_cols, squeeze=False)
    for row_idx, row in enumerate(imgs):
        row = [image] + row if with_orig else row
        for col_idx, img in enumerate(row):
            ax = axs[row_idx, col_idx]
            ax.imshow(np.asarray(img), **imshow_kwargs)
            ax.set(xticklabels=[], yticklabels=[], xticks=[], yticks=[])

    if with_orig:
        axs[0, 0].set(title='Original image')
        axs[0, 0].title.set_size(8)
    if row_title is not None:
        for row_idx in range(num_rows):
            axs[row_idx, 0].set(ylabel=row_title[row_idx])

    plt.tight_layout()

plot([get_noisy_image(x_start, torch.tensor([t])) for t in [0, 50, 100, 150, 199]])

這意味著我們現在可以根據上面定義的模型定義損失函式：

def p_losses(denoise_model, x_start, t, noise=None, loss_type="l1"):
    if noise is None:
        noise = torch.randn_like(x_start)

    x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
    predicted_noise = denoise_model(x_noisy, t)

    if loss_type == 'l1':
        loss = F.l1_loss(noise, predicted_noise)
    elif loss_type == 'l2':
        loss = F.mse_loss(noise, predicted_noise)
    elif loss_type == "huber":
        loss = F.smooth_l1_loss(noise, predicted_noise)
    else:
        raise NotImplementedError()

    return loss

`denoise_model`將是上面定義的 U-Net。我們將使用真實噪聲和預測噪聲之間的 Huber 損失。

定義 PyTorch 資料集 + DataLoader

這裡我們定義一個普通的PyTorch 資料集。該資料集簡單地由真實資料集（如 Fashion-MNIST、CIFAR-10 或 ImageNet）中的影像組成，併線性縮放到 $[−1, 1]$ 。

每個影像都被調整為相同的大小。值得注意的是，影像也會隨機水平翻轉。根據論文：

我們在 CIFAR10 訓練期間使用了隨機水平翻轉；我們嘗試了帶翻轉和不帶翻轉的訓練，發現翻轉略微改善了樣本質量。

在這裡，我們使用 🤗 Datasets 庫，輕鬆地從中心載入 Fashion MNIST 資料集。該資料集包含已經具有相同解析度（即 28x28）的影像。

from datasets import load_dataset

# load dataset from the hub
dataset = load_dataset("fashion_mnist")
image_size = 28
channels = 1
batch_size = 128

接下來，我們定義一個函式，該函式將即時應用於整個資料集。我們為此使用了 `with_transform` 功能。該函式只應用了一些基本的影像預處理：隨機水平翻轉、重新縮放，最後使它們的值在 $[-1,1]$ 範圍內。

from torchvision import transforms
from torch.utils.data import DataLoader

# define image transformations (e.g. using torchvision)
transform = Compose([
            transforms.RandomHorizontalFlip(),
            transforms.ToTensor(),
            transforms.Lambda(lambda t: (t * 2) - 1)
])

# define function
def transforms(examples):
   examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]]
   del examples["image"]

   return examples

transformed_dataset = dataset.with_transform(transforms).remove_columns("label")

# create dataloader
dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)

batch = next(iter(dataloader))
print(batch.keys())

Output:
----------------------------------------------------------------------------------------------------
dict_keys(['pixel_values'])

取樣

由於我們將在訓練期間從模型中取樣（以跟蹤進度），因此我們在下面定義了相應的程式碼。論文中將取樣總結為演算法2

從擴散模型生成新影像是透過逆轉擴散過程來實現的：我們從 $T$ 開始，從高斯分佈中取樣純噪聲，然後使用我們的神經網路逐漸對其進行去噪（使用它學到的條件機率），直到我們到達時間步 $t = 0$ 。如上所示，我們可以透過插入均值的重引數化，使用我們的噪聲預測器，推匯出稍微不那麼去噪的影像 $\mathbf{x}_{t-1 }$ 。請記住，方差是提前已知的。

理想情況下，我們最終得到的影像看起來像是來自真實資料分佈的。

下面的程式碼實現了這一點。

@torch.no_grad()
def p_sample(model, x, t, t_index):
    betas_t = extract(betas, t, x.shape)
    sqrt_one_minus_alphas_cumprod_t = extract(
        sqrt_one_minus_alphas_cumprod, t, x.shape
    )
    sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
    
    # Equation 11 in the paper
    # Use our model (noise predictor) to predict the mean
    model_mean = sqrt_recip_alphas_t * (
        x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t
    )

    if t_index == 0:
        return model_mean
    else:
        posterior_variance_t = extract(posterior_variance, t, x.shape)
        noise = torch.randn_like(x)
        # Algorithm 2 line 4:
        return model_mean + torch.sqrt(posterior_variance_t) * noise 

# Algorithm 2 (including returning all images)
@torch.no_grad()
def p_sample_loop(model, shape):
    device = next(model.parameters()).device

    b = shape[0]
    # start from pure noise (for each example in the batch)
    img = torch.randn(shape, device=device)
    imgs = []

    for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
        img = p_sample(model, img, torch.full((b,), i, device=device, dtype=torch.long), i)
        imgs.append(img.cpu().numpy())
    return imgs

@torch.no_grad()
def sample(model, image_size, batch_size=16, channels=3):
    return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))

請注意，上面的程式碼是原始實現的簡化版本。我們發現我們的簡化（與論文中的演算法2一致）與原始、更復雜的實現一樣有效，後者採用了裁剪。

訓練模型

接下來，我們以常規 PyTorch 方式訓練模型。我們還定義了一些邏輯，用於使用上面定義的 `sample` 方法定期儲存生成的影像。

from pathlib import Path

def num_to_groups(num, divisor):
    groups = num // divisor
    remainder = num % divisor
    arr = [divisor] * groups
    if remainder > 0:
        arr.append(remainder)
    return arr

results_folder = Path("./results")
results_folder.mkdir(exist_ok = True)
save_and_sample_every = 1000

下面，我們定義模型，並將其移動到 GPU。我們還定義了一個標準最佳化器（Adam）。

from torch.optim import Adam

device = "cuda" if torch.cuda.is_available() else "cpu"

model = Unet(
    dim=image_size,
    channels=channels,
    dim_mults=(1, 2, 4,)
)
model.to(device)

optimizer = Adam(model.parameters(), lr=1e-3)

我們開始訓練吧！

from torchvision.utils import save_image

epochs = 6

for epoch in range(epochs):
    for step, batch in enumerate(dataloader):
      optimizer.zero_grad()

      batch_size = batch["pixel_values"].shape[0]
      batch = batch["pixel_values"].to(device)

      # Algorithm 1 line 3: sample t uniformally for every example in the batch
      t = torch.randint(0, timesteps, (batch_size,), device=device).long()

      loss = p_losses(model, batch, t, loss_type="huber")

      if step % 100 == 0:
        print("Loss:", loss.item())

      loss.backward()
      optimizer.step()

      # save generated images
      if step != 0 and step % save_and_sample_every == 0:
        milestone = step // save_and_sample_every
        batches = num_to_groups(4, batch_size)
        all_images_list = list(map(lambda n: sample(model, batch_size=n, channels=channels), batches))
        all_images = torch.cat(all_images_list, dim=0)
        all_images = (all_images + 1) * 0.5
        save_image(all_images, str(results_folder / f'sample-{milestone}.png'), nrow = 6)

Output:
----------------------------------------------------------------------------------------------------
Loss: 0.46477368474006653
Loss: 0.12143351882696152
Loss: 0.08106148988008499
Loss: 0.0801810547709465
Loss: 0.06122320517897606
Loss: 0.06310459971427917
Loss: 0.05681884288787842
Loss: 0.05729678273200989
Loss: 0.05497899278998375
Loss: 0.04439849033951759
Loss: 0.05415581166744232
Loss: 0.06020551547408104
Loss: 0.046830907464027405
Loss: 0.051029372960329056
Loss: 0.0478244312107563
Loss: 0.046767622232437134
Loss: 0.04305662214756012
Loss: 0.05216279625892639
Loss: 0.04748568311333656
Loss: 0.05107741802930832
Loss: 0.04588869959115982
Loss: 0.043014321476221085
Loss: 0.046371955424547195
Loss: 0.04952816292643547
Loss: 0.04472338408231735

取樣（推理）

要從模型中取樣，我們可以直接使用上面定義的取樣函式

# sample 64 images
samples = sample(model, image_size=image_size, batch_size=64, channels=channels)

# show a random one
random_index = 5
plt.imshow(samples[-1][random_index].reshape(image_size, image_size, channels), cmap="gray")

看起來模型能夠生成一件漂亮的 T 恤！請記住，我們訓練的資料集解析度相當低 (28x28)。

我們還可以建立去噪過程的 GIF

import matplotlib.animation as animation

random_index = 53

fig = plt.figure()
ims = []
for i in range(timesteps):
    im = plt.imshow(samples[i][random_index].reshape(image_size, image_size, channels), cmap="gray", animated=True)
    ims.append([im])

animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)
animate.save('diffusion.gif')
plt.show()

後續閱讀

請注意，DDPM 論文表明擴散模型是（無）條件影像生成的一個有前途的方向。此後，這一領域（極大地）得到了改進，尤其是在文字條件影像生成方面。下面，我們列出了一些重要的（但遠非詳盡的）後續工作

改進的去噪擴散機率模型 (Nichol 等人，2021)：發現學習條件分佈的方差（除了均值）有助於提高效能
用於高保真影像生成的級聯擴散模型 (Ho 等人，2021)：引入了級聯擴散，它包含多個擴散模型的管道，這些模型生成解析度不斷提高的影像，用於高保真影像合成
擴散模型在影像合成方面擊敗 GANs (Dhariwal 等人，2021)：透過改進 U-Net 架構並引入分類器引導，表明擴散模型可以實現優於當前最先進生成模型的影像樣本質量
無分類器擴散引導 (Ho 等人，2021)：透過使用單個神經網路聯合訓練條件和無條件擴散模型，表明您不需要分類器來引導擴散模型
使用 CLIP 潛在變數進行分層文字條件影像生成 (DALL-E 2) (Ramesh 等人，2022)：使用先驗將文字描述轉換為 CLIP 影像嵌入，然後擴散模型將其解碼為影像
具有深度語言理解的光逼真文字到影像擴散模型 (ImageGen) (Saharia 等人，2022)：表明將大型預訓練語言模型（例如 T5）與級聯擴散相結合在文字到影像合成方面效果很好