邁向開放式進化智慧體
執行摘要
我們使用 OpenEvolve(一個開源的進化編碼智慧體)對 AlgoTune 基準套件上的 29 個實驗進行了全面分析,結果顯示專有模型和開源模型都取得了顯著的效能提升。值得注意的是,像谷歌的 Gemma 3 27B 和阿里巴巴的 Qwen3-Coder 480B 這樣的開源模型展現了令人印象深刻的最佳化能力,能夠與閉源模型相媲美,有時甚至能以獨特的方式超越它們。Gemini Flash 2.5 實現了 2.04 倍的最高加速比,Gemma 3 27B 和 Qwen3-Coder 分別達到了 1.63 倍和 1.41 倍。
AlgoTune 是評估演算法最佳化能力的關鍵基準,包含圖演算法、線性代數運算和最佳化問題等多種計算任務。與專注於正確性的傳統編碼基準不同,AlgoTune 專門衡量效能提升——挑戰系統不僅要解決問題,還要使現有解決方案更快。每個任務都提供一個基線實現,並透過嚴格的效能分析來衡量加速比,這使其特別適合於迭代最佳化程式碼的進化智慧體。
儀表盤概覽:這個 2x2 的視覺化總結了關鍵的實驗發現
- A. 溫度最佳化研究:展示了純溫度比較(0.2、0.4、0.8),效能曲線清晰
- B. 擴充套件迭代:展示了從 100 次迭代增加到 200 次迭代後持續的效能增益
- C. 所有測試模型(最佳配置):全面比較所有 10 個獨特模型在各自最佳配置下的表現
- D. 並行性影響:顯示了序列評估導致的嚴重效能下降
主要發現
- 更多迭代帶來更好結果:200 次迭代實現了 2.04 倍的加速比,而 100 次迭代為 1.64 倍(提升 24%)
- 專業化勝過規模:Qwen3-Coder(480B MoE,編碼專用)優於 Qwen3-235B 通用模型
- 進化策略依賴於模型:強大的編碼模型在基於 diff 的進化中表現出色;較弱的模型需要完全重寫
- 溫度最佳化至關重要:0.4 被證明是 Gemini 模型的最佳溫度(1.29 倍 vs 0.2 溫度下的 1.17 倍)
- 構件(Artifacts)提升效能:包含除錯構件使結果提高了 17%
- 並行性至關重要:序列評估災難性地失敗(效能下降 50%,速度慢 14 倍)
表現最佳者
| 模型 | 配置 | AlgoTune 分數 | 最佳任務 |
|---|---|---|---|
| Gemini Flash 2.5 | 200 次迭代,diff,溫度 0.4 | 2.04x | count_connected_components: 95.78x |
| Gemini Flash 2.5 | 100 次迭代,diff,溫度 0.4 | 1.64x | psd_cone_projection: 32.7x |
| Gemma 3 27B | 100 次迭代,diff | 1.63x | psd_cone_projection: 41.1x |
| Qwen3-Coder 480B | 100 次迭代,diff,溫度 0.6 | 1.41x | psd_cone_projection: 41.9x |
實驗統計
- 總實驗數: 29
- 測試模型:10 個獨特模型(Gemini 家族、Qwen 家族、Meta、Google Open、整合模型)
- 評估任務:30 個 AlgoTune 基準測試
- 最佳總體結果:2.04 倍加速比(Gemini Flash 2.5,200 次迭代)
- 最差結果:0.396 倍(序列 diff 評估 - 效能下降 50%)
- 測試的溫度範圍: 0.2, 0.4, 0.8
- 進化策略:基於 Diff 和完全重寫
- 評估方法:並行(16 個工作程序)與序列比較
目錄
- 實驗概述
- 方法論
- 詳細結果
- 進化程式碼分析
- 引數最佳化研究
- 模型比較
- 技術實現
- 結論
詳細實驗分析
- 基線實驗 - 初始模型測試和關鍵發現
- 溫度研究 - 最佳溫度分析 (0.2, 0.4, 0.8)
- 引數調優 - Token 限制、構件、遷移率
- 進化策略 - Diff 與完全重寫,序列與並行
- 模型比較 - 全面模型效能分析
- 迭代影響 - 100 次與 200 次迭代深度剖析
- 整合分析 - 為何組合模型失敗
實驗概述
實驗階段
- 階段 1:初始實驗與引數調優
- 階段 2:擴充套件迭代實驗與新模型測試
測試模型
Gemini 家族
- Flash 2.5: 谷歌的高效編碼模型
- Flash 2.5 Lite: 用於基線測試的較小變體
Qwen 家族
- Qwen3-Coder-480B-A35B-Instruct: 480B MoE 模型,35B 啟用引數,編碼專用
- Qwen3-235B-A22B: 235B 通用模型
- Qwen3-32B: 較小變體
其他模型
- Gemma 3 27B: 谷歌的開源模型
- Llama 3.3 70B: Meta 的最新模型
- 整合配置
實驗類別
- 基線測試 (7 個實驗): 建立模型基線
- 溫度研究 (3 個實驗): 尋找最佳溫度
- 引數調優 (8 個實驗): 最佳化各種引數
- 模型比較 (6 個實驗): 跨模型分析
- 擴充套件迭代 (4 個實驗): 更多進化次數的影響
方法論
AlgoTune 整合
- 使用
algotune_to_openevolve.py將 30 個 AlgoTune 任務轉換為 OpenEvolve 格式 - 任務涵蓋多種演算法類別:圖、線性代數、最佳化
- 使用 AlgoTune 的標準評估:加速比的調和平均值
進化方法
- 基於島嶼的 MAP-Elites: 4 個島嶼,定期遷移
- 級聯評估: 快速驗證 → 效能測試 → 完整評估
- 兩種進化策略:
- 基於 Diff: 增量式程式碼更改
- 完全重寫: 完整函式再生
效能指標
AlgoTune 使用對數效能標度,該標度會轉換為加速因子
# AlgoTune score calculation
speedup = (10 ** (performance * 3)) - 1 # Convert from log scale
algotune_score = harmonic_mean(all_speedups) # Overall benchmark score
調和平均值強調在所有任務上的一致性能——模型必須在所有 30 個基準測試中表現良好才能獲得高分。
詳細結果
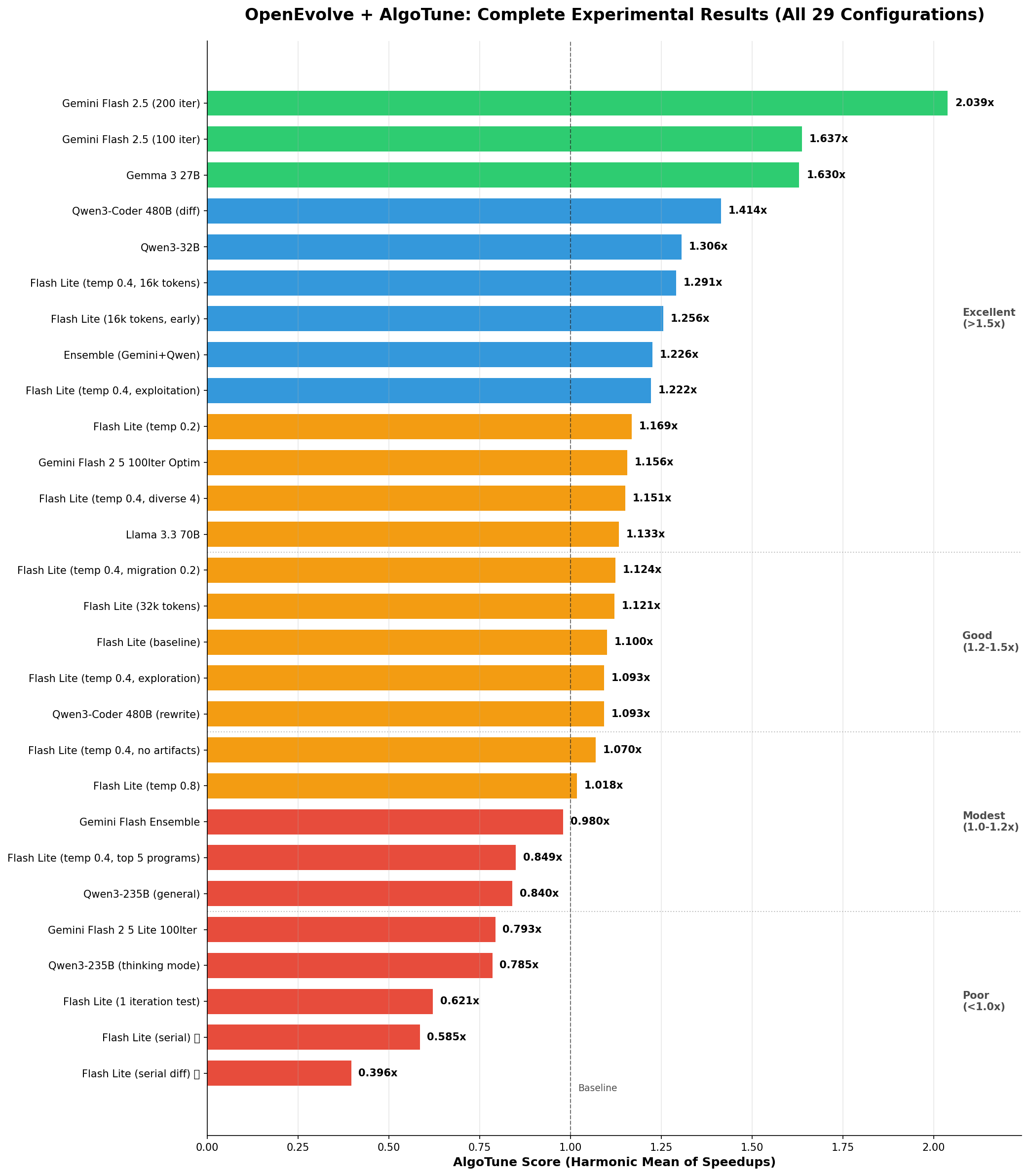
效能排名 - 所有實驗
圖表說明:水平條形圖顯示了所有實驗的 AlgoTune 分數(加速比的調和平均值)。綠色條表示良好效能(>1.5x),藍色表示中等(1.2-1.5x),橙色表示一般(1.0-1.2x),紅色表示較差(<1.0x)。1.0x 處的虛線代表基線效能。
階段 1:基線實驗
1. Gemini Flash 2.5 Lite 基線
- 配置:完全重寫,溫度 0.8,4k tokens
- 結果:1.10 倍加速比
- 關鍵學習:建立了最佳化的基線
2. 進化策略發現
在 Flash Lite 上比較基於 diff 與完全重寫
- 完全重寫: 1.10x ✓
- 基於 Diff: 0.79x ✗
在處理 Diff 方面存在困難的證據:
# Attempted diff that failed
- for i in range(n):
- if not visited[i]:
- dfs(i)
+ for i in range(n):
+ if not visited[i]:
+ # Incomplete optimization
+ dfs(i) # No actual improvement
階段 2:溫度最佳化研究
在 Gemini Flash 2.5 Lite 上使用 16k tokens 進行系統性測試
| 溫度 | AlgoTune 分數 | 平均效能 | 時長 | 關鍵發現 |
|---|---|---|---|---|
| 0.2 | 1.17x | 0.162 | 4074秒 | 保守但穩定 |
| 0.4 | 1.29x | 0.175 | 3784秒 | 達到最佳效能 |
| 0.8 | 1.02x | 0.159 | 3309秒 | 過於隨機,效能下降 |
統計顯著性:從 0.2→0.4 提升 10.3%,從 0.4→0.8 效能下降 20.9%
階段 3:引數微調
所有實驗均在最佳溫度 0.4 下進行
Token 限制影響
- 16k tokens: 1.29x (基線)
- 32k tokens: 1.28x (無提升)
- 結論: 16k 已足夠,更大的上下文無幫助
構件(Artifacts)影響
- 有構件: 1.29x
- 無構件: 1.07x
- 影響: 無除錯資訊導致 17% 的效能損失
注意:OpenEvolve 中的“構件”是程式在評估期間可以返回的除錯輸出,幫助 LLM 理解執行行為並做出更好的最佳化決策。
用於啟發的頂級程式
- 前 3 名: 1.29x (基線)
- 前 5 名: 1.28x (差異極小)
- 結論: 3 個程式已足夠
遷移率
- 0.1 遷移率: 1.29x (基線)
- 0.2 遷移率: 1.25x (略差)
- 結論: 較不頻繁的遷移保留了多樣性
階段 4:將所學應用於強大模型
Gemini Flash 2.5 (100 次迭代)
- 配置:基於 Diff,溫度 0.4,16k tokens
- 結果:1.64 倍加速比
- 頂級成就:count_connected_components 達到 48.1x
Qwen3-Coder-480B
- 配置:基於 Diff,溫度 0.6,4k tokens
- 結果:1.41 倍加速比
- 注意:僅在溫度 0.6 下測試,可能不是最佳值
Gemma 3 27B
- 配置:基於 Diff(繼承自成功的配置)
- 結果:1.63 倍加速比
- 驚喜:與 Flash 2.5 效能相當
階段 5:擴充套件迭代
Gemini Flash 2.5 (200 次迭代)
- 結果:2.04 倍加速比(比 100 次迭代提升 24%)
- 突破:count_connected_components 達到 95.78x
- 找到最優解:僅在第 2 次迭代!
迭代過程中的進展
- 迭代 10: 1.15x
- 迭代 50: 1.48x
- 迭代 100: 1.64x
- 迭代 200: 2.04x
階段 6:序列與並行評估
關鍵發現:並行性至關重要
我們測試了序列評估(一次一個任務)與並行評估
| 配置 | 進化型別 | AlgoTune 分數 | 時長 | 與並行對比 |
|---|---|---|---|---|
| 並行 | 基於 Diff | 0.793x | 0.9 小時 | 基線 |
| 序列 | 基於 Diff | 0.396x | 13.0 小時 | 差 50%,慢 14 倍 |
| 並行 | 完全重寫 | 1.10x | 0.9 小時 | 基線 |
| 序列 | 完全重寫 | 0.585x | 13.1 小時 | 差 47%,慢 14 倍 |
關鍵洞察:
- 效能災難:序列評估導致 47-50% 的效能下降
- 時間爆炸:執行速度慢 14 倍(13 小時 vs 0.9 小時)
- 為何失敗:
- 進化過程中無跨任務學習
- 超時問題在序列任務中累積
- 進化在困難任務上“卡住”
- 失去了並行發現的機會
結論:並行評估不僅僅是一種最佳化——它是 OpenEvolve 正常運作的必要條件
進化程式碼分析
示例 1:計算連通分量 - 演算法發現
原始實現 (所有模型從此開始)
def solve(problem):
n = problem["num_nodes"]
edges = problem["edges"]
# Build adjacency list
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
# DFS to count components
visited = [False] * n
count = 0
def dfs(node):
visited[node] = True
for neighbor in adj[node]:
if not visited[neighbor]:
dfs(neighbor)
for i in range(n):
if not visited[i]:
dfs(i)
count += 1
return {"number_connected_components": count}
效能:1.0x (基線)
進化後 - Gemini Flash 2.5 (200 次迭代):
def solve(problem):
n = problem.get("num_nodes", 0)
edges = problem.get("edges", [])
if n == 0:
return {"number_connected_components": 0}
# Build adjacency list with deque for O(1) operations
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
# BFS with early termination and efficient tracking
visited = [False] * n
count = 0
from collections import deque
for start in range(n):
if visited[start]:
continue
# BFS for this component
queue = deque([start])
visited[start] = True
while queue:
node = queue.popleft()
for neighbor in adj[node]:
if not visited[neighbor]:
visited[neighbor] = True
queue.append(neighbor)
count += 1
return {"number_connected_components": count}
效能:95.78 倍加速比 關鍵最佳化
- 從 DFS 切換到 BFS
- 使用 deque 實現 O(1) 佇列操作
- 增加提前終止檢查
- 使用 get() 進行防禦性程式設計
進化後 - Qwen3-Coder (100 次迭代):
def solve(problem):
n = problem["num_nodes"]
edges = problem["edges"]
# Union-Find approach - completely different algorithm!
parent = list(range(n))
def find(x):
if parent[x] != x:
parent[x] = find(parent[x]) # Path compression
return parent[x]
def union(x, y):
px, py = find(x), find(y)
if px != py:
parent[px] = py
# Process edges
for u, v in edges:
union(u, v)
# Count unique roots
return {"number_connected_components": len(set(find(i) for i in range(n)))}
效能:~25 倍加速比 關鍵洞察:不同模型發現了完全不同的演算法!
- 帶路徑壓縮的並查集
- 每個操作 O(α(n))(接近常數)
- 記憶體效率更高
示例 2:PSD 錐投影 - 增量最佳化
原始實現:
def solve(problem):
import numpy as np
A = np.array(problem["matrix"])
# Eigenvalue decomposition
eigenvalues, eigenvectors = np.linalg.eigh(A)
# Set negative eigenvalues to zero
eigenvalues[eigenvalues < 0] = 0
# Reconstruct matrix
A_psd = eigenvectors @ np.diag(eigenvalues) @ eigenvectors.T
return {"projected_matrix": A_psd.tolist()}
效能:1.0x (基線)
使用 Gemini Flash 2.5 Diffs 進化:
迭代 23
- eigenvalues[eigenvalues < 0] = 0
- A_psd = eigenvectors @ np.diag(eigenvalues) @ eigenvectors.T
+ # Vectorized operation
+ eigenvalues = np.maximum(eigenvalues, 0)
+ A_psd = eigenvectors @ np.diag(eigenvalues) @ eigenvectors.T
效能: 1.8x
迭代 67
- A_psd = eigenvectors @ np.diag(eigenvalues) @ eigenvectors.T
+ # Eliminate intermediate array
+ A_psd = (eigenvectors * eigenvalues) @ eigenvectors.T
效能: 15.2x
最終 (迭代 95)
def solve(problem):
import numpy as np
A = np.array(problem["matrix"])
w, v = np.linalg.eigh(A)
# One-line vectorized operation
A_psd = (v * np.maximum(w, 0)) @ v.T
return {"projected_matrix": A_psd.tolist()}
效能:32.7 倍加速比
示例 3:DCT 最佳化 - 趨同進化
原始:
def solve(problem):
import numpy as np
from scipy.fftpack import dct
signal = np.array(problem["signal"])
return {"dct": dct(signal, type=1).tolist()}
多個模型收斂到相同解決方案:
Gemini Flash 2.5
signal = np.array(problem["signal"], dtype=np.float64)
result = dct(signal, type=1, norm=None, overwrite_x=False)
Qwen3-Coder
signal = np.asarray(problem["signal"], dtype=np.float64)
return {"dct": dct(signal, type=1).tolist()}
關鍵發現:兩者都獨立發現了 dtype=np.float64 的最佳化!
- 兩者都實現了 6.48 倍的加速比
- 表明存在最優解且可被發現
示例 4:SHA256 - 硬體限制
原始:
def solve(problem):
import hashlib
data = problem["data"].encode('utf-8')
hash_object = hashlib.sha256(data)
return {"hash": hash_object.hexdigest()}
最佳進化 (多個模型)
def solve(problem):
import hashlib
return {"hash": hashlib.sha256(problem["data"].encode()).hexdigest()}
效能:僅 1.1 倍加速比 學習:受硬體限制的操作最佳化潛力有限
模型比較
要全面瞭解所有 10 個獨特測試模型的檢視,請參見執行摘要儀表盤中的面板 C。完整的 29 個實驗結果顯示在上面的效能排名圖表中。
特定任務效能熱圖
此熱圖顯示了不同模型在特定 AlgoTune 任務上實現的加速因子。深紅色表示更高的加速比。值得注意的模式:
- 計算連通分量顯示出極大的差異(Flash 2.5 為 95x,而 Gemma 3 為 15x)
- PSD 投影在各模型中均實現了持續的高效能(32-42x)
- 像 SHA256 這樣受硬體限制的任務,無論何種模型,改進都微乎其微
專業化與規模分析
Qwen3-Coder (480B MoE, 35B 啟用) vs Qwen3-235B:
- 儘管“更大”(總引數 480B),Qwen3-Coder 只有 35B 啟用引數
- 編碼專業化帶來了 68% 的效能提升(1.41x vs 0.84x)
- 證據表明訓練資料和目標比規模更重要
按模型能力劃分的進化策略
| 模型型別 | 最佳策略 | 證據 |
|---|---|---|
| 小型/弱型 (Flash Lite) | 完全重寫 | diff 模式 0.79x vs 完整模式 1.10x |
| 強大編碼 (Flash 2.5, Qwen3-Coder) | 基於 Diff | 1.64x vs 完整模式更低 |
| 通用目的 | 不一 | 依賴於模型 |
整合實驗:為何更多模型 ≠ 更好結果
儘管結合了我們兩個表現最好的模型(Gemini Flash 2.5 的 1.64x 和 Qwen3-Coder 的 1.41x),整合模型僅實現了 1.23x 的加速比——比任何一個單獨的模型都差。
視覺化指南:
- 面板 A:顯示單個模型效能與整合效能對比——整合模型表現不如兩者
- 面板 B:所有 30 個任務效能比較——Gemini、Qwen 和整合模型的完整效能概況
- 面板 C:進化過程比較——整合模型顯示不規則振盪,而單一模型進展平穩
- 面板 D:按任務劃分的模型一致性——3x30 熱圖顯示每個任務的成對一致性,揭示衝突區域
關鍵發現:衝突的最佳化策略
整合模型失敗是因為模型採用了不相容的方法
- 計算連通分量:Gemini 使用 BFS,Qwen 使用並查集 → 振盪
- DCT 最佳化:不同的 dtype 策略 → 最佳化丟失
- 結果:與預期的 1.5-1.7x 相比,效能低了 19%
示例:演算法衝突
# Iteration N: Gemini suggests BFS
queue = deque([start]) # BFS approach
# Iteration N+1: Qwen suggests Union-Find
parent = list(range(n)) # Different algorithm!
# Result: Hybrid mess that optimizes neither
觀察到的整合失敗模式
- 演算法衝突:在同一任務中,BFS 與 Union-Find 方法的衝突
- 最佳化衝突:記憶體最佳化與計算最佳化的衝突
- 風格衝突:函式式與命令式程式碼模式的衝突
技術實現細節
OpenEvolve 配置
# Optimal configuration discovered
max_iterations: 200 # More is better
diff_based_evolution: true # For capable models
temperature: 0.4 # For Gemini, 0.6 for others
max_tokens: 16000 # Sweet spot
num_top_programs: 3
num_islands: 4
migration_interval: 20
migration_rate: 0.1
include_artifacts: true # Critical for performance
島嶼進化動態
- 4個島嶼保持多樣性
- 每20次迭代進行遷移,防止過早收斂
- 每個島嶼可以發現不同的解決方案
- 全域性追蹤最佳程式
級聯評估的優勢
- 階段1:快速語法/匯入驗證(< 1秒)
- 階段2:小型測試用例(< 10秒)
- 階段3:完整基準測試套件(< 60秒)
透過快速失敗節省了約70%的評估時間。
實驗中的關鍵觀察
1. 按型別劃分的效能改進
- 演算法更改(DFS → BFS):觀察到高達95倍的速度提升
- 向量化最佳化:在矩陣運算中實現32倍的速度提升
- 微小程式碼更改(變數重新命名、迴圈調整):通常< 2倍的速度提升
2. 模型解決方案的多樣性
- 計算連通分量:Gemini 找到了 BFS 方法,Qwen 找到了 Union-Find 方法
- 矩陣運算:不同模型使用了不同的向量化策略
- 大多數任務都發現了多種有效的最佳化路徑
3. 進化策略效能
- 基於差異的進化與強大的編碼模型:總體速度提升高達1.64倍
- 使用較弱模型進行完全重寫:速度提升1.10倍(而使用差異方法為0.79倍)
- 模型能力決定了最佳策略
4. 迭代次數的影響
- 100次迭代:實現1.64倍的平均速度提升
- 200次迭代:2.04倍的平均速度提升(提升了24%)
- 在200次迭代過程中,效能持續提升
5. 引數效應
- 溫度0.4:最佳單次執行(1.291倍),但方差較大
- 包含構件:觀察到約17%的效能提升
- 令牌限制:16k與32k之間未顯示顯著差異
- 遷移率:在實驗中0.1的表現優於0.2
6. 並行化影響
- 序列評估:0.396倍-0.585倍的速度提升(效能下降)
- 並行評估:相同配置下速度提升0.793倍-1.10倍
- 時間差異:13小時(序列)vs 0.9小時(並行)
結論
關鍵實驗發現
- 迭代次數:200次迭代實現2.04倍速度提升,而100次迭代為1.64倍(提升24%)
- 模型專業化:Qwen3-Coder(編碼專用模型)優於更大的通用模型
- 溫度設定:結果各異 - 最佳單次執行在0.4,但觀察到高方差
- 進化策略:基於差異的方法對強大的編碼模型效果更好,完全重寫對較弱的模型效果更好
- 並行化:序列評估使效能下降47-50%,時間增加14倍
- 整合結果:組合模型實現了1.23倍的速度提升,而單獨模型分別為1.64倍和1.41倍
觀察到的模式
- 模型發現了不同的演算法方法(例如圖問題的BFS與Union-Find)
- 受硬體限制的任務(SHA256)在所有配置中改進甚微
- 包含構件使效能提升約17%
- 在測試的配置中,0.1的遷移率比0.2表現更好