基於 Transformer 的編碼器-解碼器模型

!pip install transformers==4.2.1
!pip install sentencepiece==0.1.95

基於 Transformer 的編碼器-解碼器模型由 Vaswani 等人在著名的論文 《Attention is all you need》 中提出，如今已成為自然語言處理（NLP）領域中事實上的標準編碼器-解碼器架構。

近來，針對基於 Transformer 的編碼器-解碼器模型，學界湧現了大量關於不同預訓練目標的研究，例如 T5、Bart、Pegasus、ProphetNet、Marge 等，但模型架構基本保持不變。

本博文旨在詳細解釋基於 Transformer 的編碼器-解碼器架構是如何為*序列到序列（sequence-to-sequence）*問題建模的。我們將重點關注該架構定義的數學模型，以及如何在推理過程中使用該模型。在此過程中，我們會介紹一些 NLP 領域序列到序列模型的背景知識，並將基於 Transformer 的編碼器-解碼器架構分解為編碼器和解碼器兩部分進行剖析。我們提供了大量插圖，並將基於 Transformer 的編碼器-解碼器模型的理論與其在 🤗Transformers 中的推理實踐聯絡起來。請注意，本博文不解釋如何訓練此類模型——這將是未來一篇博文的主題。

基於 Transformer 的編碼器-解碼器模型是多年來在表示學習和模型架構方面研究的成果。本 notebook 簡要總結了神經編碼器-解碼器模型的歷史。若想了解更多背景，建議讀者閱讀 Sebastion Ruder 這篇精彩的博文。此外，建議讀者對自注意力架構有基本瞭解。Jay Alammar 的這篇博文可以很好地幫助大家回顧原始的 Transformer 模型。

在撰寫本 notebook 時，🤗Transformers 包含了 T5、Bart、MarianMT 和 Pegasus 等編碼器-解碼器模型，相關文件的模型總結部分對此有概述。

本 notebook 分為四個部分：

• 背景 - 簡要介紹神經編碼器-解碼器模型的歷史，重點關注基於 RNN 的模型。
• 編碼器-解碼器 - 介紹基於 Transformer 的編碼器-解碼器模型，並解釋該模型如何用於推理。
• 編碼器 - 詳細解釋模型的編碼器部分。
• 解碼器 - 詳細解釋模型的解碼器部分。

每個部分都建立在前一部分的基礎上，但也可以獨立閱讀。

背景

自然語言生成（NLG）是 NLP 的一個子領域，其中的任務最適合用序列到序列問題來表達。這類任務可以定義為找到一個能將輸入詞序列對映到目標詞序列的模型。一些經典例子是摘要和翻譯。下文中，我們假設每個詞都被編碼成一個向量表示。$n$ 個輸入詞因此可以表示為一個由 $n$ 個輸入向量組成的序列：

$$\mathbf{X}_{1:n} = \{\mathbf{x}_1, \ldots, \mathbf{x}_n\}.$$

因此，序列到序列問題可以透過尋找一個從 $n$ 個向量的輸入序列 $\mathbf{X}_{1:n}$ 到 $m$ 個目標向量的序列 $\mathbf{Y}_{1:m}$ 的對映 $f$ 來解決，其中目標向量的數量 $m$ 是事先未知的，並取決於輸入序列：

$$f: \mathbf{X}_{1:n} \to \mathbf{Y}_{1:m}.$$

Sutskever 等人 (2014) 指出，深度神經網路 (DNN)，“*儘管具有靈活性和強大能力，但只能定義一種輸入和目標都能用固定維度向量合理編碼的對映。*”${}^1$

使用 DNN 模型 ${}^2$ 解決序列到序列問題將意味著目標向量的數量 $m$ 必須是*事先*已知的，並且必須獨立於輸入 $\mathbf{X}_{1:n}$。這並非最優，因為對於 NLG 任務，目標詞的數量通常取決於輸入 $\mathbf{X}_{1:n}$ 的內容，而不僅僅是輸入長度 $n$。例如，一篇 1000 詞的文章可以被總結為 200 詞，也可以是 100 詞，這取決於其內容。

2014 年，Cho 等人和 Sutskever 等人提出使用純粹基於迴圈神經網路 (RNN) 的編碼器-解碼器模型來處理*序列到序列*任務。與 DNN 不同，RNN 能夠對對映到可變數量目標向量的問題進行建模。讓我們更深入地瞭解一下基於 RNN 的編碼器-解碼器模型的工作原理。

在推理過程中，編碼器 RNN 透過相繼更新其*隱藏狀態*${}^3$ 來編碼一個輸入序列 $\mathbf{X}_{1:n}$。在處理完最後一個輸入向量 $\mathbf{x}_n$ 後，編碼器的隱藏狀態定義了輸入編碼 $\mathbf{c}$。因此，編碼器定義瞭如下對映：

$$f_{\theta_{enc}}: \mathbf{X}_{1:n} \to \mathbf{c}.$$

然後，用輸入編碼初始化解碼器的隱藏狀態，在推理過程中，解碼器 RNN 被用來以自迴歸的方式生成目標序列。下面我們來解釋一下。

在數學上，解碼器定義了在給定隱藏狀態 $\mathbf{c}$ 的情況下，目標序列 $\mathbf{Y}_{1:m}$ 的機率分佈：

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c}).$$

根據貝葉斯法則，該分佈可以分解為單個目標向量的條件分佈，如下所示：

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c}) = \prod_{i=1}^{m} p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}).$$

因此，如果該架構能夠對給定所有先前目標向量的下一個目標向量的條件分佈進行建模：

$$p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}), \forall i \in \{1, \ldots, m\},$$

那麼它就可以透過簡單地將所有條件機率相乘來對給定隱藏狀態 $\mathbf{c}$ 的任何目標向量序列的分佈進行建模。

那麼，基於 RNN 的解碼器架構是如何對 $p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c})$ 進行建模的呢？

在計算上，模型將前一個內部隱藏狀態 $\mathbf{c}_{i-1}$ 和前一個目標向量 $\mathbf{y}_{i-1}$ 依次對映到當前的內部隱藏狀態 $\mathbf{c}_i$ 和一個 logit 向量 $\mathbf{l}_i$（下圖中用深紅色表示）：

$$f_{\theta_{\text{dec}}}(\mathbf{y}_{i-1}, \mathbf{c}_{i-1}) \to \mathbf{l}_i, \mathbf{c}_i.$$ 這裡的 $\mathbf{c}_0$ 被定義為 $\mathbf{c}$，即基於 RNN 的編碼器的輸出隱藏狀態。隨後，使用 softmax 操作將 logit 向量 $\mathbf{l}_i$ 轉換為下一個目標向量的條件機率分佈：

$$p(\mathbf{y}_i | \mathbf{l}_i) = \textbf{Softmax}(\mathbf{l}_i), \text{ with } \mathbf{l}_i = f_{\theta_{\text{dec}}}(\mathbf{y}_{i-1}, \mathbf{c}_{\text{prev}}).$$

有關 logit 向量和最終機率分佈的更多細節，請參見腳註${}^4$。從上面的方程我們可以看出，當前目標向量 $\mathbf{y}_i$ 的分佈直接以先前目標向量 $\mathbf{y}_{i-1}$ 和先前隱藏狀態 $\mathbf{c}_{i-1}$ 為條件。因為先前隱藏狀態 $\mathbf{c}_{i-1}$ 依賴於所有先前的目標向量 $\mathbf{y}_0, \ldots, \mathbf{y}_{i-2}$，可以說基於 RNN 的解碼器是*隱式地*（即*間接地*）對條件分佈 $p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c})$ 進行建模。

可能的目標向量序列 $\mathbf{Y}_{1:m}$ 的空間非常大，以至於在推理時，必須依賴解碼方法 ${}^5$ 來有效地從 $p_{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c})$ 中取樣高機率的目標向量序列。

給定這樣的解碼方法，在推理過程中，下一個輸入向量 $\mathbf{y}_i$ 可以從 $p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c})$ 中取樣，然後被追加到輸入序列中，這樣解碼器 RNN 就可以對 $p_{\theta_{\text{dec}}}(\mathbf{y}_{i+1} | \mathbf{Y}_{0: i}, \mathbf{c})$ 進行建模，以*自迴歸*的方式取樣下一個輸入向量 $\mathbf{y}_{i+1}$，依此類推。

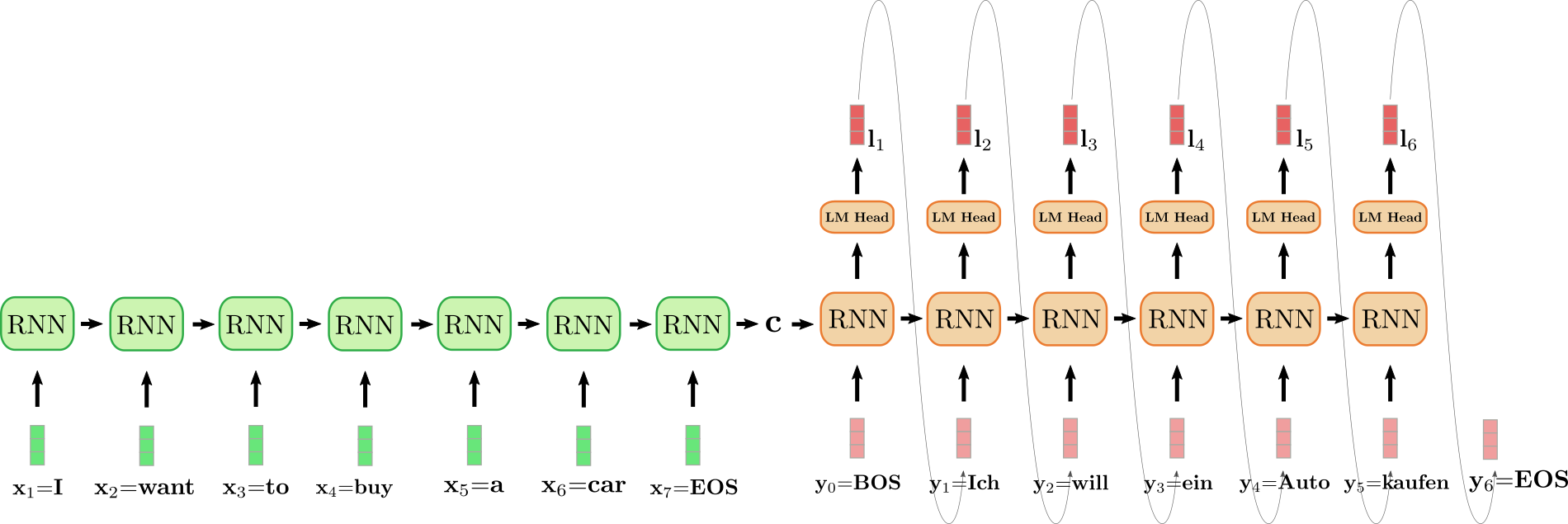
基於 RNN 的編碼器-解碼器模型的一個重要特點是定義了*特殊*向量，例如 $\text{EOS}$ 和 $\text{BOS}$ 向量。$\text{EOS}$ 向量通常表示最後的輸入向量 $\mathbf{x}_n$，用於“提示”編碼器輸入序列已結束，並且也定義了目標序列的結尾。一旦從 logit 向量中取樣得到 $\text{EOS}$，生成過程就完成了。$\text{BOS}$ 向量表示在解碼的第一步輸入到解碼器 RNN 的輸入向量 $\mathbf{y}_0$。為了輸出第一個 logit $\mathbf{l}_1$，需要一個輸入，但由於第一步還沒有生成任何輸入，因此將一個特殊的 $\text{BOS}$ 輸入向量送入解碼器 RNN。好吧 - 相當複雜！讓我們透過一個例子來闡述和逐步分析。

展開的 RNN 編碼器用綠色表示，展開的 RNN 解碼器用紅色表示。

英文句子 "I want to buy a car"，表示為 $\mathbf{x}_1 = \text{I}$、$\mathbf{x}_2 = \text{want}$、$\mathbf{x}_3 = \text{to}$、$\mathbf{x}_4 = \text{buy}$、$\mathbf{x}_5 = \text{a}$、$\mathbf{x}_6 = \text{car}$ 和 $\mathbf{x}_7 = \text{EOS}$ 被翻譯成德語："Ich will ein Auto kaufen"，定義為 $\mathbf{y}_0 = \text{BOS}$、$\mathbf{y}_1 = \text{Ich}$、$\mathbf{y}_2 = \text{will}$、$\mathbf{y}_3 = \text{ein}$、$\mathbf{y}_4 = \text{Auto}, \mathbf{y}_5 = \text{kaufen}$ 以及 $\mathbf{y}_6=\text{EOS}$。首先，輸入向量 $\mathbf{x}_1 = \text{I}$ 由編碼器 RNN 處理並更新其隱藏狀態。請注意，因為我們只對編碼器最終的隱藏狀態 $\mathbf{c}$ 感興趣，所以我們可以忽略 RNN 編碼器的目標向量。然後編碼器 RNN 以同樣的方式處理輸入句子的其餘部分 $\text{want}$, $\text{to}$, $\text{buy}$, $\text{a}$, $\text{car}$, $\text{EOS}$，在每一步都更新其隱藏狀態，直到到達向量 $\mathbf{x}_7={EOS}$${}^6$。在上圖中，連線展開的編碼器 RNN 的水平箭頭表示隱藏狀態的順序更新。編碼器 RNN 的最終隱藏狀態由 $\mathbf{c}$ 表示，它完全定義了輸入序列的*編碼*，並用作解碼器 RNN 的初始隱藏狀態。這可以看作是在編碼後的輸入上*調節*解碼器 RNN。

為了生成第一個目標向量，解碼器接收 $\text{BOS}$ 向量，在上圖設計中表示為 $\mathbf{y}_0$。然後，RNN 的目標向量透過*語言模型頭部 (LM Head)* 前饋層進一步對映到 logit 向量 $\mathbf{l}_1$，以定義第一個目標向量的條件分佈，如上所述

$$p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{c}).$$

單詞 $\text{Ich}$ 被取樣（由連線 $\mathbf{l}_1$ 和 $\mathbf{y}_1$ 的灰色箭頭表示），因此可以對第二個目標向量進行取樣

$$\text{will} \sim p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \text{Ich}, \mathbf{c}).$$

以此類推，直到第 $i=6$ 步，從 $\mathbf{l}_6$ 中取樣得到 $\text{EOS}$ 向量，解碼過程結束。最終的目標序列為 $\mathbf{Y}_{1:6} = \{\mathbf{y}_1, \ldots, \mathbf{y}_6\}$，在我們上面的例子中即 "Ich will ein Auto kaufen"。

總而言之，一個基於 RNN 的編碼器-解碼器模型，由 $f_{\theta_{\text{enc}}}$ 和 $p_{\theta_{\text{dec}}}$ 表示，它透過分解的方式定義了分佈 $p(\mathbf{Y}_{1:m} | \mathbf{X}_{1:n})$

$$p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{Y}_{1:m} | \mathbf{X}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{X}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}), \text{ with } \mathbf{c}=f_{\theta_{enc}}(X).$$

在推理過程中，高效的解碼方法可以自迴歸地生成目標序列 $\mathbf{Y}_{1:m}$。

基於 RNN 的編碼器-解碼器模型席捲了 NLG 社群。2016 年，谷歌宣佈將完全用一個基於 RNN 的編碼器-解碼器模型來取代其經過大量特徵工程的翻譯服務（參見此處）。

儘管如此，基於 RNN 的編碼器-解碼器模型有兩個缺陷。首先，RNN 存在梯度消失問題，這使得捕捉長程依賴關係變得非常困難，參見 Hochreiter et al. (2001)。其次，RNN 固有的迴圈架構在編碼時阻礙了有效的並行化，參見 Vaswani et al. (2017)。

---

${}^1$ 論文中的原話是“*儘管 DNN 具有靈活性和強大能力，但它們只能應用於輸入和目標可以被合理地編碼為固定維度向量的問題*”，此處略有改動。

${}^2$ 對於卷積神經網路 (CNN)，情況也基本相同。雖然可變長度的輸入序列可以被送入 CNN，但目標的維度將始終依賴於輸入的維度或固定為特定值。

${}^3$ 在第一步，隱藏狀態被初始化為零向量，並與第一個輸入向量 $\mathbf{x}_1$ 一起送入 RNN。

${}^4$ 神經網路可以定義所有單詞的機率分佈，即 $p(\mathbf{y} | \mathbf{c}, \mathbf{Y}_{0: i-1})$，過程如下。首先，網路定義一個從輸入 $\mathbf{c}, \mathbf{Y}_{0: i-1}$ 到嵌入向量表示 $\mathbf{y'}$ 的對映，這對應於 RNN 的目標向量。然後將嵌入向量表示 $\mathbf{y'}$ 傳遞給“語言模型頭部 (language model head)”層，這意味著它將與*詞嵌入矩陣*相乘，即 $\mathbf{Y}^{\text{vocab}}$，從而計算出 $\mathbf{y'}$ 與每個編碼向量 $\mathbf{y} \in \mathbf{Y}^{\text{vocab}}$ 之間的分數。得到的向量稱為 logit 向量 $\mathbf{l} = \mathbf{Y}^{\text{vocab}} \mathbf{y'}$，它可以透過應用 softmax 操作對映到所有單詞的機率分佈：$p(\mathbf{y} | \mathbf{c}) = \text{Softmax}(\mathbf{Y}^{\text{vocab}} \mathbf{y'}) = \text{Softmax}(\mathbf{l})$。

${}^5$ 集束搜尋解碼 (Beam-search decoding) 就是這樣一種解碼方法的例子。不同的解碼方法超出了本筆記的範圍。建議讀者參考這篇關於解碼方法的互動式筆記。

${}^6$ Sutskever 等人 (2014) 的工作將輸入序列進行了反轉，因此在上面的示例中，輸入向量將對應於 $\mathbf{x}_1 = \text{car}$、$\mathbf{x}_2 = \text{a}$、$\mathbf{x}_3 = \text{buy}$、$\mathbf{x}_4 = \text{to}$、$\mathbf{x}_5 = \text{want}$、$\mathbf{x}_6 = \text{I}$ 以及 $\mathbf{x}_7 = \text{EOS}$。這樣做的動機是為了讓對應的詞對（例如 $\mathbf{x}_6 = \text{I}$ 和 $\mathbf{y}_1 = \text{Ich}$）之間建立更短的連線。該研究小組強調，反轉輸入序列是其模型在機器翻譯任務上效能提升的一個關鍵原因。

編碼器-解碼器

2017 年，Vaswani 等人引入了 Transformer，從而催生了*基於 Transformer* 的編碼器-解碼器模型。

與基於 RNN 的編碼器-解碼器模型類似，基於 Transformer 的編碼器-解碼器模型也由一個編碼器和一個解碼器組成，兩者都是*殘差注意力塊 (residual attention blocks)* 的堆疊。基於 Transformer 的編碼器-解碼器模型的關鍵創新在於，這種殘差注意力塊可以在不表現出迴圈結構的情況下處理可變長度 $n$ 的輸入序列 $\mathbf{X}_{1:n}$。不依賴迴圈結構使得基於 Transformer 的編碼器-解碼器能夠高度並行化，這讓該模型在現代硬體上的計算效率比基於 RNN 的編碼器-解碼器模型高出幾個數量級。

提醒一下，為了解決*序列到序列*問題，我們需要找到一個從輸入序列 $\mathbf{X}_{1:n}$ 到可變長度 $m$ 的輸出序列 $\mathbf{Y}_{1:m}$ 的對映。讓我們看看如何使用基於 Transformer 的編碼器-解碼器模型來找到這種對映。

與基於 RNN 的編碼器-解碼器模型類似，基於 Transformer 的編碼器-解碼器模型定義了給定輸入序列 $\mathbf{X}_{1:n}$ 的目標向量 $\mathbf{Y}_{1:m}$ 的條件分佈：

$$p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{Y}_{1:m} | \mathbf{X}_{1:n}).$$

基於 Transformer 的編碼器部分將輸入序列 $\mathbf{X}_{1:n}$ 編碼為一個*隱藏狀態序列* $\mathbf{\overline{X}}_{1:n}$，從而定義了對映

$$f_{\theta_{\text{enc}}}: \mathbf{X}_{1:n} \to \mathbf{\overline{X}}_{1:n}.$$

然後，基於 Transformer 的解碼器部分對給定編碼隱藏狀態序列 $\mathbf{\overline{X}}_{1:n}$ 的目標向量序列 $\mathbf{Y}_{1:n}$ 進行條件機率分佈建模

$$p_{\theta_{dec}}(\mathbf{Y}_{1:n} | \mathbf{\overline{X}}_{1:n}).$$

根據貝葉斯法則，這個分佈可以被分解為目標向量 $\mathbf{y}_i$ 在給定編碼隱藏狀態 $\mathbf{\overline{X}}_{1:n}$ 和所有先前目標向量 $\mathbf{Y}_{0:i-1}$ 的條件機率分佈的乘積：

$$p_{\theta_{dec}}(\mathbf{Y}_{1:n} | \mathbf{\overline{X}}_{1:n}) = \prod_{i=1}^{n} p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}).$$

在此，基於 Transformer 的解碼器將編碼的隱藏狀態序列 $\mathbf{\overline{X}}_{1:n}$ 和所有先前已生成的目標向量 $\mathbf{Y}_{0:i-1}$ 對映到 *logit* 向量 $\mathbf{l}_i$。然後，logit 向量 $\mathbf{l}_i$ 經過 *softmax* 操作處理，以定義條件分佈 $p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n})$，就像對基於 RNN 的解碼器所做的那樣。然而，與基於 RNN 的解碼器不同，目標向量 $\mathbf{y}_i$ 的分佈*明確地*（或直接地）以所有先前的目標向量 $\mathbf{y}_0, \ldots, \mathbf{y}_{i-1}$ 為條件，我們稍後會更詳細地看到這一點。第 0 個目標向量 $\mathbf{y}_0$ 在這裡由一個特殊的“句子開始”$\text{BOS}$ 向量表示。

定義了條件分佈 $p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n})$ 後，我們現在可以在推理時*自迴歸地*生成輸出，從而定義從輸入序列 $\mathbf{X}_{1:n}$ 到輸出序列 $\mathbf{Y}_{1:m}$ 的對映。

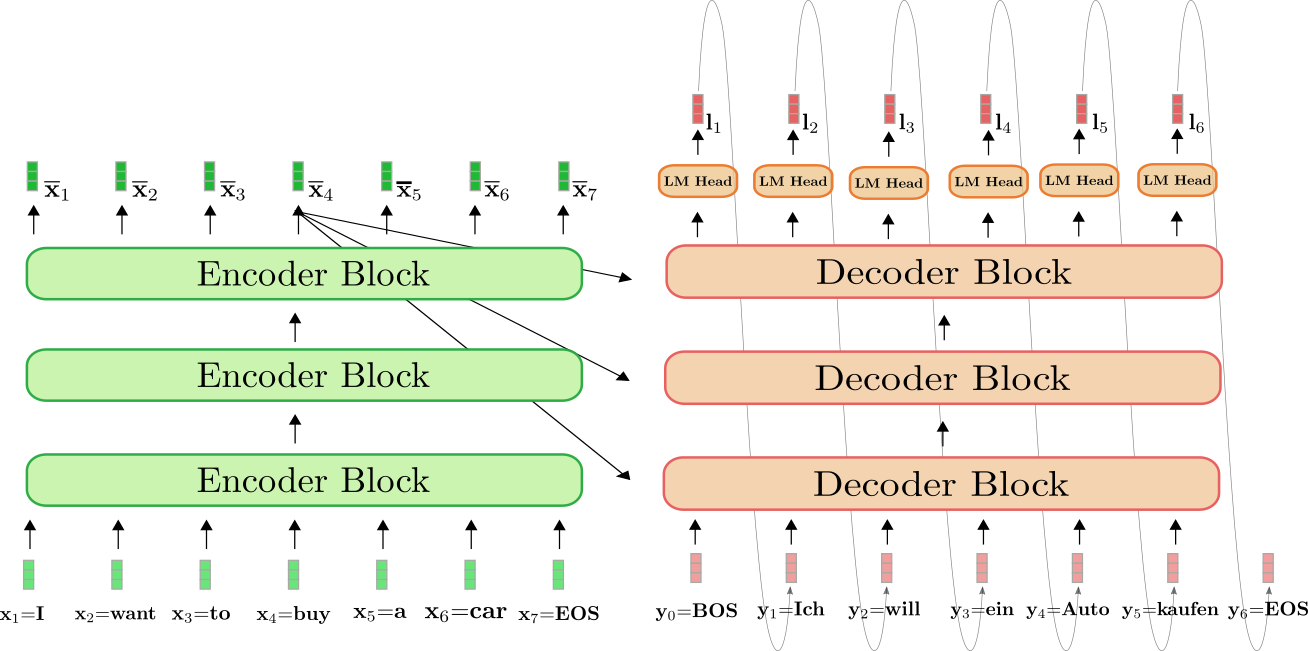
讓我們將基於 Transformer 的編碼器-解碼器模型的*自迴歸*生成全過程視覺化。

基於 Transformer 的編碼器以綠色顯示，基於 Transformer 的解碼器以紅色顯示。與上一節一樣，我們展示了英語句子“I want to buy a car”如何被翻譯成德語“Ich will ein Auto kaufen”。該英語句子由 $\mathbf{x}_1 = \text{I}$、$\mathbf{x}_2 = \text{want}$、$\mathbf{x}_3 = \text{to}$、$\mathbf{x}_4 = \text{buy}$、$\mathbf{x}_5 = \text{a}$、$\mathbf{x}_6 = \text{car}$ 和 $\mathbf{x}_7 = \text{EOS}$表示，德語翻譯則由 $\mathbf{y}_0 = \text{BOS}$、$\mathbf{y}_1 = \text{Ich}$、$\mathbf{y}_2 = \text{will}$、$\mathbf{y}_3 = \text{ein}$、$\mathbf{y}_4 = \text{Auto}, \mathbf{y}_5 = \text{kaufen}$ 和 $\mathbf{y}_6=\text{EOS}$ 定義。

首先，編碼器處理完整的輸入序列 $\mathbf{X}_{1:7}$ = "I want to buy a car"（由淺綠色向量表示），將其轉換為一個帶上下文的編碼序列 $\mathbf{\overline{X}}_{1:7}$。例如，$\mathbf{\overline{x}}_4$ 定義了一個編碼，該編碼不僅依賴於輸入 $\mathbf{x}_4$ = "buy"，還依賴於所有其他詞 "I", "want", "to", "a", "car" 和 "EOS"，即上下文。

接下來，輸入編碼 $\mathbf{\overline{X}}_{1:7}$ 和 BOS 向量，即 $\mathbf{y}_0$，一起被送入解碼器。解碼器處理輸入 $\mathbf{\overline{X}}_{1:7}$ 和 $\mathbf{y}_0$，得到第一個 logit $\mathbf{l}_1$（以深紅色顯示），以定義第一個目標向量 $\mathbf{y}_1$ 的條件分佈

$$p_{\theta_{enc, dec}}(\mathbf{y} | \mathbf{y}_0, \mathbf{X}_{1:7}) = p_{\theta_{enc, dec}}(\mathbf{y} | \text{BOS}, \text{I want to buy a car EOS}) = p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{\overline{X}}_{1:7}).$$

接下來，從分佈中取樣第一個目標向量 $\mathbf{y}_1$ = $\text{Ich}$（由灰色箭頭表示），現在可以再次將其送入解碼器。解碼器現在處理 $\mathbf{y}_0$ = "BOS" 和 $\mathbf{y}_1$ = "Ich" 來定義第二個目標向量 $\mathbf{y}_2$ 的條件分佈

$$p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich}, \mathbf{\overline{X}}_{1:7}).$$

我們可以再次取樣並生成目標向量 $\mathbf{y}_2$ = "will"。我們以自迴歸的方式繼續，直到在第 6 步從條件分佈中取樣到 EOS 向量

$$\text{EOS} \sim p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7}).$$

依此類推，以自迴歸的方式進行。

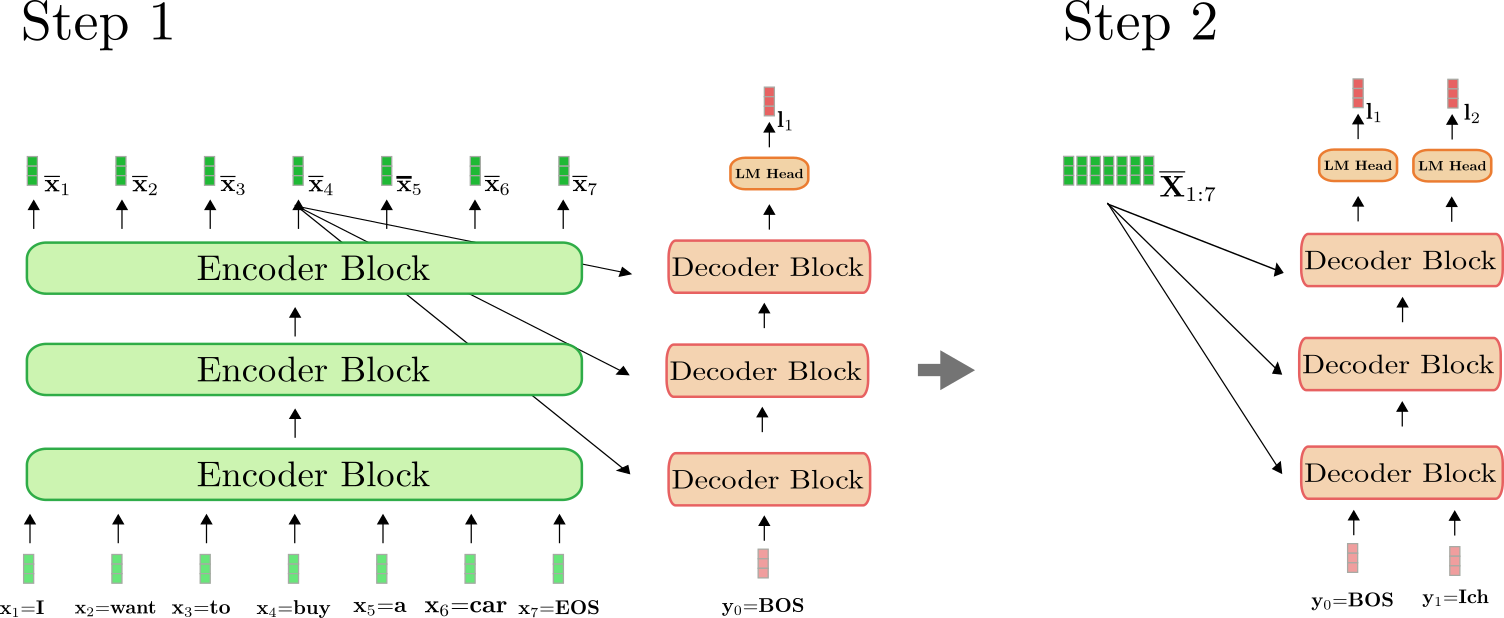
重要的是要理解，編碼器僅在第一次前向傳播中使用，用於將 $\mathbf{X}_{1:n}$ 對映到 $\mathbf{\overline{X}}_{1:n}$。從第二次前向傳播開始，解碼器可以直接利用之前計算的編碼 $\mathbf{\overline{X}}_{1:n}$。為清楚起見，讓我們為上面的示例說明第一次和第二次前向傳播。

可以看出，只有在步驟 $i=1$ 中，我們才需要將“I want to buy a car EOS”編碼為 $\mathbf{\overline{X}}_{1:7}$。在步驟 $i=2$ 中，“I want to buy a car EOS”的上下文編碼被解碼器直接重用。

在 🤗Transformers 中，這種自迴歸生成是在呼叫 .generate() 方法時在幕後完成的。讓我們使用我們的一個翻譯模型來實際操作一下。

from transformers import MarianMTModel, MarianTokenizer

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# translate example
output_ids = model.generate(input_ids)[0]

# decode and print
print(tokenizer.decode(output_ids))

輸出

    <pad> Ich will ein Auto kaufen

呼叫 .generate() 在幕後做了很多事情。首先，它將 input_ids 傳遞給編碼器。其次，它將一個預定義的標記（在 MarianMTModel 的情況下是 $\text{<pad>}$ 符號）連同編碼後的 input_ids 一起傳遞給解碼器。第三，它應用集束搜尋（beam search）解碼機制，根據最後一個解碼器輸出${}^1$自迴歸地取樣下一個輸出詞。有關集束搜尋解碼工作原理的更多詳細資訊，建議閱讀這篇部落格文章。

在附錄中，我們提供了一個程式碼片段，展示瞭如何“從頭開始”實現一個簡單的生成方法。為了完全理解自迴歸生成在幕後是如何工作的，強烈建議閱讀附錄。

總結一下：

• 基於 Transformer 的編碼器定義了從輸入序列 $\mathbf{X}_{1:n}$ 到上下文編碼序列 $\mathbf{\overline{X}}_{1:n}$ 的對映。
• 基於 Transformer 的解碼器定義了條件分佈 $p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n})$。
• 給定一個合適的解碼機制，輸出序列 $\mathbf{Y}_{1:m}$ 可以從 $p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}), \forall i \in \{1, \ldots, m\}$ 自迴歸地取樣得到。

太好了，現在我們對基於 Transformer 的編碼器-解碼器模型的工作原理有了大致的瞭解，我們可以深入研究模型的編碼器和解碼器部分了。更具體地說，我們將看到編碼器如何利用自注意力層來產生上下文相關的向量編碼序列，以及自注意力層如何實現高效的並行化。然後，我們將詳細解釋自注意力層在解碼器模型中是如何工作的，以及解碼器如何透過交叉注意力層來依賴編碼器的輸出，以定義條件分佈 $p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n})$。在此過程中，基於 Transformer 的編碼器-解碼器模型如何解決基於 RNN 的編碼器-解碼器模型的長程依賴問題將變得顯而易見。

---

${}^1$ 對於 "Helsinki-NLP/opus-mt-en-de"，解碼引數可以在這裡訪問，我們可以看到該模型使用了 num_beams=6 的集束搜尋。

編碼器

如上一節所述，基於 Transformer 的編碼器將輸入序列對映到上下文編碼序列

$$f_{\theta_{\text{enc}}}: \mathbf{X}_{1:n} \to \mathbf{\overline{X}}_{1:n}.$$

仔細觀察架構，基於 Transformer 的編碼器是殘差連線的編碼器塊的堆疊。每個編碼器塊由一個雙向自注意力層和兩個前饋層組成。為簡單起見，我們在本筆記本中忽略歸一化層。此外，我們將不再進一步討論兩個前饋層的作用，而只是將其視為每個編碼器塊中所需的最終向量到向量的對映${}^1$。雙向自注意力層將每個輸入向量 $\mathbf{x'}_j, \forall j \in \{1, \ldots, n\}$ 與所有輸入向量 $\mathbf{x'}_1, \ldots, \mathbf{x'}_n$ 相關聯，透過這種方式將輸入向量 $\mathbf{x'}_j$ 轉換為一個更“精煉”的自身上下文表示，定義為 $\mathbf{x''}_j$。因此，第一個編碼器塊將輸入序列 $\mathbf{X}_{1:n}$（下圖中淺綠色所示）的每個輸入向量從與上下文無關的向量表示轉換為與上下文相關的向量表示，接下來的編碼器塊會進一步精煉這種上下文表示，直到最後一個編碼器塊輸出最終的上下文編碼 $\mathbf{\overline{X}}_{1:n}$（下圖中深綠色所示）。

讓我們視覺化編碼器如何將輸入序列“I want to buy a car EOS”處理成一個上下文編碼序列。與基於 RNN 的編碼器類似，基於 Transformer 的編碼器也在輸入序列中新增一個特殊的“序列結束”輸入向量，以提示模型輸入向量序列已結束${}^2$。

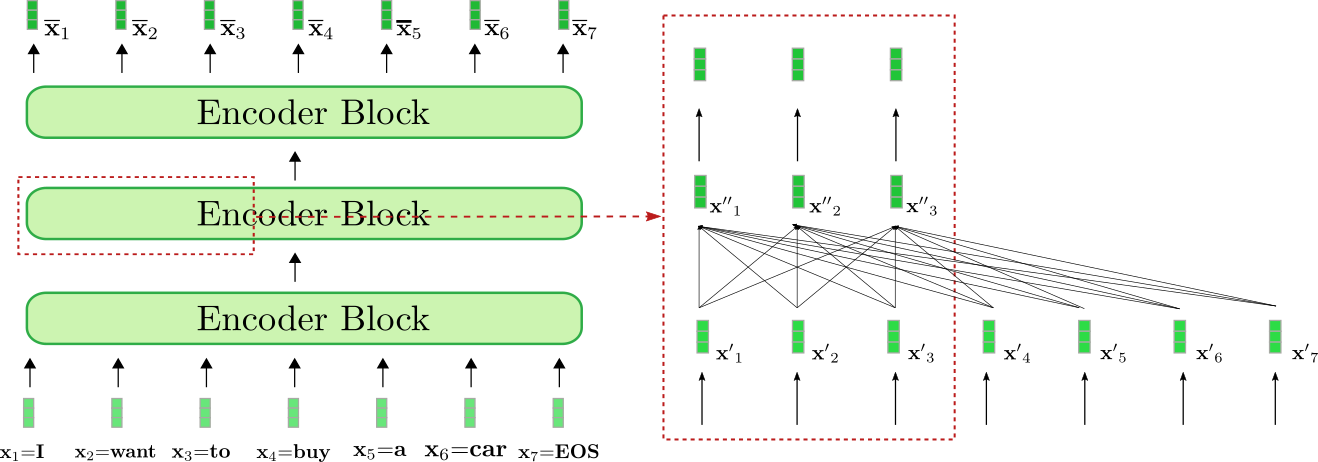
我們的示例基於 Transformer 的編碼器由三個編碼器塊組成，其中第二個編碼器塊在右側的紅色框中更詳細地顯示了前三個輸入向量 $\mathbf{x}_1, \mathbf{x}_2 and \mathbf{x}_3$。雙向自注意力機制由紅色框下部的全連線圖表示，兩個前饋層顯示在紅色框的上部。如前所述，我們將只關注雙向自注意力機制。

可以看出，自注意力層的每個輸出向量 $\mathbf{x''}_i, \forall i \in \{1, \ldots, 7\}$ 都直接依賴於所有輸入向量 $\mathbf{x'}_1, \ldots, \mathbf{x'}_7$。這意味著，例如，“want”這個詞的輸入向量表示，即 $\mathbf{x'}_2$，與“buy”這個詞，即 $\mathbf{x'}_4$ 建立了直接關係，同時也與“I”這個詞，即 $\mathbf{x'}_1$ 建立了關係。“want”的輸出向量表示，即 $\mathbf{x''}_2$，因此為“want”這個詞提供了一個更精細的上下文表示。

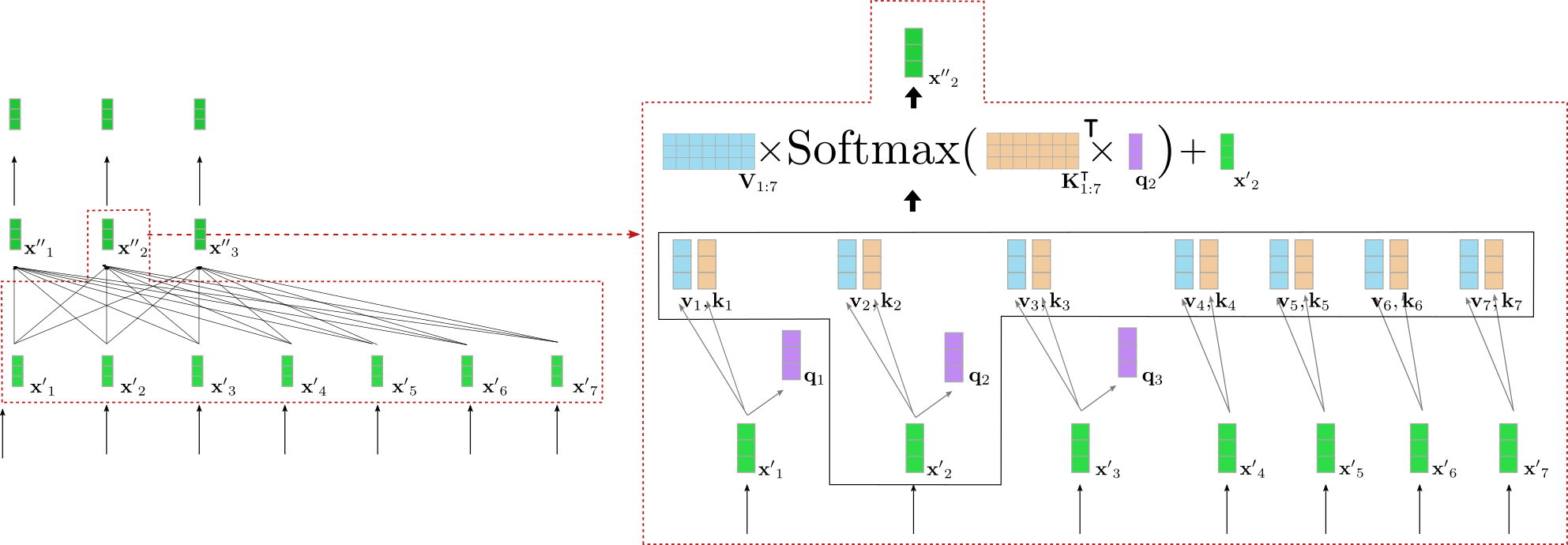
讓我們來深入瞭解一下雙向自注意力機制是如何工作的。對於編碼器塊中的輸入序列 $\mathbf{X'}_{1:n}$ 中的每個輸入向量 $\mathbf{x'}_i$，會透過三個可訓練的權重矩陣 $\mathbf{W}_q, \mathbf{W}_v, \mathbf{W}_k$ 分別投影成一個鍵向量 $\mathbf{k}_i$、一個值向量 $\mathbf{v}_i$ 和一個查詢向量 $\mathbf{q}_i$（下圖中分別以橙色、藍色和紫色表示）。

$$\mathbf{q}_i = \mathbf{W}_q \mathbf{x'}_i,$$ $$\mathbf{v}_i = \mathbf{W}_v \mathbf{x'}_i,$$ $$\mathbf{k}_i = \mathbf{W}_k \mathbf{x'}_i,$$ $$\forall i \in \{1, \ldots n \}.$$

注意，相同的權重矩陣被應用於每個輸入向量 $\mathbf{x}_i, \forall i \in \{i, \ldots, n\}$。在將每個輸入向量 $\mathbf{x}_i$ 投影到查詢向量、鍵向量和值向量之後，每個查詢向量 $\mathbf{q}_j, \forall j \in \{1, \ldots, n\}$ 會與所有的鍵向量 $\mathbf{k}_1, \ldots, \mathbf{k}_n$ 進行比較。鍵向量 $\mathbf{k}_1, \ldots \mathbf{k}_n$ 中與查詢向量 $\mathbf{q}_j$ 越相似，則其對應的值向量 $\mathbf{v}_j$ 對輸出向量 $\mathbf{x''}_j$ 越重要。更具體地說，一個輸出向量 $\mathbf{x''}_j$ 被定義為所有值向量 $\mathbf{v}_1, \ldots, \mathbf{v}_n$ 的加權和，再加上輸入向量 $\mathbf{x'}_j$。其中的權重與 $\mathbf{q}_j$ 和各自的鍵向量 $\mathbf{k}_1, \ldots, \mathbf{k}_n$ 之間的餘弦相似度成正比，數學上表示為 $\textbf{Softmax}(\mathbf{K}_{1:n}^\intercal \mathbf{q}_j)$，如下面的方程所示。要全面瞭解自注意力層，建議讀者閱讀這篇部落格文章或原始論文。

好的，這聽起來相當複雜。讓我們為上面例子中的一個查詢向量來圖解說明雙向自注意力層。為簡單起見，我們假設示例中基於 transformer 的解碼器只使用一個注意力頭 config.num_heads = 1 並且沒有應用歸一化。

左側再次顯示了之前圖示的第二個編碼器塊，右側則詳細展示了針對第二個輸入向量 $\mathbf{x'}_2$（對應輸入詞“want”）的雙向自注意力機制。首先，所有輸入向量 $\mathbf{x'}_1, \ldots, \mathbf{x'}_7$ 被投影成各自的查詢向量 $\mathbf{q}_1, \ldots, \mathbf{q}_7$（上圖中僅顯示前三個查詢向量，以紫色表示）、值向量 $\mathbf{v}_1, \ldots, \mathbf{v}_7$（以藍色表示）和鍵向量 $\mathbf{k}_1, \ldots, \mathbf{k}_7$（以橙色表示）。然後查詢向量 $\mathbf{q}_2$ 與所有鍵向量的轉置相乘，即 $\mathbf{K}_{1:7}^{\intercal}$，隨後進行 softmax 操作以得到自注意力權重。最後，將自注意力權重與相應的值向量相乘，並加上輸入向量 $\mathbf{x'}_2$，以輸出“want”這個詞的“精煉”表示，即 $\mathbf{x''}_2$（右側以深綠色顯示）。整個方程在右側方框的上半部分進行了圖解。透過 $\mathbf{K}_{1:7}^{\intercal}$ 和 $\mathbf{q}_2$ 的相乘，使得“want”的向量表示可以與所有其他輸入詞“I”、“to”、“buy”、“a”、“car”、“EOS”的向量表示進行比較，從而自注意力權重反映了其他每個輸入向量表示 $\mathbf{x'}_j \text{, with } j \ne 2$ 對於“want”的精煉表示 $\mathbf{x''}_2$ 的重要性。

為了進一步理解雙向自注意力層的影響，讓我們假設處理以下句子：“The house is beautiful and well located in the middle of the city where it is easily accessible by public transport”（這所房子很漂亮，位置很好，在市中心，公共交通很方便）。單詞“it”指的是“house”，兩者相隔12個“位置”。在基於transformer的編碼器中，雙向自注意力層僅透過一次數學運算就能將“house”的輸入向量與“it”的輸入向量關聯起來（可與本節第一個圖示進行比較）。相比之下，在基於RNN的編碼器中，一個相隔12個“位置”的詞至少需要12次數學運算，這意味著在基於RNN的編碼器中，需要線性數量的數學運算。這使得基於RNN的編碼器更難建模長距離的上下文表示。此外，很明顯，基於transformer的編碼器比基於RNN的編解碼器模型更不容易丟失重要資訊，因為編碼的序列長度保持不變，即 $\textbf{len}(\mathbf{X}_{1:n}) = \textbf{len}(\mathbf{\overline{X}}_{1:n}) = n$，而RNN將長度從 $*\textbf{len}((\mathbf{X}_{1:n}) = n$ 壓縮到僅為 $\textbf{len}(\mathbf{c}) = 1$，這使得RNN很難有效地編碼輸入詞之間的長距離依賴關係。

除了更容易學習長距離依賴關係外，我們還可以看到Transformer架構能夠並行處理文字。從數學上講，這可以透過將自注意力公式寫成查詢、鍵和值矩陣的乘積來輕鬆證明。

$$\mathbf{X''}_{1:n} = \mathbf{V}_{1:n} \text{Softmax}(\mathbf{Q}_{1:n}^\intercal \mathbf{K}_{1:n}) + \mathbf{X'}_{1:n}.$$

輸出 $\mathbf{X''}_{1:n} = \mathbf{x''}_1, \ldots, \mathbf{x''}_n$ 是透過一系列矩陣乘法和一個可以有效並行化的 softmax 操作計算出來的。請注意，在基於 RNN 的編碼器模型中，隱藏狀態 $\mathbf{c}$ 的計算必須按順序進行：計算第一個輸入向量 $\mathbf{x}_1$ 的隱藏狀態，然後計算第二個輸入向量的隱藏狀態，該狀態依賴於第一個隱藏向量的隱藏狀態，依此類推。RNN 的順序性使其無法有效並行化，與基於 Transformer 的編碼器模型相比，在現代 GPU 硬體上的效率要低得多。

很好，現在我們應該對 a) 基於 Transformer 的編碼器模型如何有效建模長程上下文表示，以及 b) 它們如何高效處理長序列輸入向量有了更好的理解。

現在，讓我們編寫一個我們 MarianMT 編碼器-解碼器模型中編碼器部分的簡短示例，以驗證所解釋的理論在實踐中是否成立。

---

${}^1$ 關於前饋層在基於 Transformer 的模型中所扮演角色的詳細解釋超出了本筆記的範圍。在 Yun 等人 (2017) 的文章中指出，前饋層對於將每個上下文向量 $\mathbf{x'}_i$ 單獨對映到所需的輸出空間至關重要，而*自注意力*層本身無法做到這一點。這裡應該注意，每個輸出標記 $\mathbf{x'}$ 都由相同的前饋層處理。更多細節，建議讀者閱讀該論文。

${}^2$ 然而，EOS 輸入向量不必附加到輸入序列中，但在許多情況下已被證明可以提高效能。與此相反，基於 Transformer 的解碼器的第 0 個 $\text{BOS}$ 目標向量是必需的，作為預測第一個目標向量的起始輸入向量。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

embeddings = model.get_input_embeddings()

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# pass input_ids to encoder
encoder_hidden_states = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state

# change the input slightly and pass to encoder
input_ids_perturbed = tokenizer("I want to buy a house", return_tensors="pt").input_ids
encoder_hidden_states_perturbed = model.base_model.encoder(input_ids_perturbed, return_dict=True).last_hidden_state

# compare shape and encoding of first vector
print(f"Length of input embeddings {embeddings(input_ids).shape[1]}. Length of encoder_hidden_states {encoder_hidden_states.shape[1]}")

# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `I` equal to its perturbed version?: ", torch.allclose(encoder_hidden_states[0, 0], encoder_hidden_states_perturbed[0, 0], atol=1e-3))

輸出

    Length of input embeddings 7. Length of encoder_hidden_states 7
    Is encoding for `I` equal to its perturbed version?:  False

我們比較輸入詞嵌入的長度，即 embeddings(input_ids)，它對應於 $\mathbf{X}_{1:n}$，與 encoder_hidden_states 的長度，它對應於 $\mathbf{\overline{X}}_{1:n}$。此外，我們還將詞序列“I want to buy a car”和其微擾版本“I want to buy a house”透過編碼器傳遞，以檢查當輸入序列中僅最後一個詞發生改變時，第一個輸出編碼（對應於“I”）是否會不同。

正如預期的那樣，輸入詞嵌入的輸出長度和編碼器輸出編碼的長度，即 $\textbf{len}(\mathbf{X}_{1:n})$ 和 $\textbf{len}(\mathbf{\overline{X}}_{1:n})$ 是相等的。其次，可以注意到，當最後一個詞從 "car" 變為 "house" 時，$\mathbf{\overline{x}}_1 = \text{"I"}$ 的編碼輸出向量的值是不同的。然而，如果理解了雙向自注意力，這應該不足為奇。

附帶一提，諸如 BERT 之類的*自編碼*模型與*基於 Transformer 的*編碼器模型具有完全相同的架構。*自編碼*模型利用這種架構在開放領域的文字資料上進行大規模的自監督預訓練，從而可以將任何詞序列對映到深層的雙向表示。在 Devlin 等人 (2018) 的研究中，作者表明，一個預訓練的 BERT 模型，在其之上增加一個單一的特定任務分類層，可以在十一項 NLP 任務上取得最先進的結果。🤗Transformers 的所有*自編碼*模型都可以在這裡找到。

解碼器

如*編碼器-解碼器*部分所述，*基於 Transformer 的*解碼器定義了在給定上下文化編碼序列的情況下目標序列的條件機率分佈

$$p_{\theta_{dec}}(\mathbf{Y}_{1: m} | \mathbf{\overline{X}}_{1:n}),$$

根據貝葉斯法則，可以將其分解為下一個目標向量的條件分佈的乘積，條件是上下文化編碼序列和所有先前的目標向量

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} | \mathbf{\overline{X}}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{dec}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}).$$

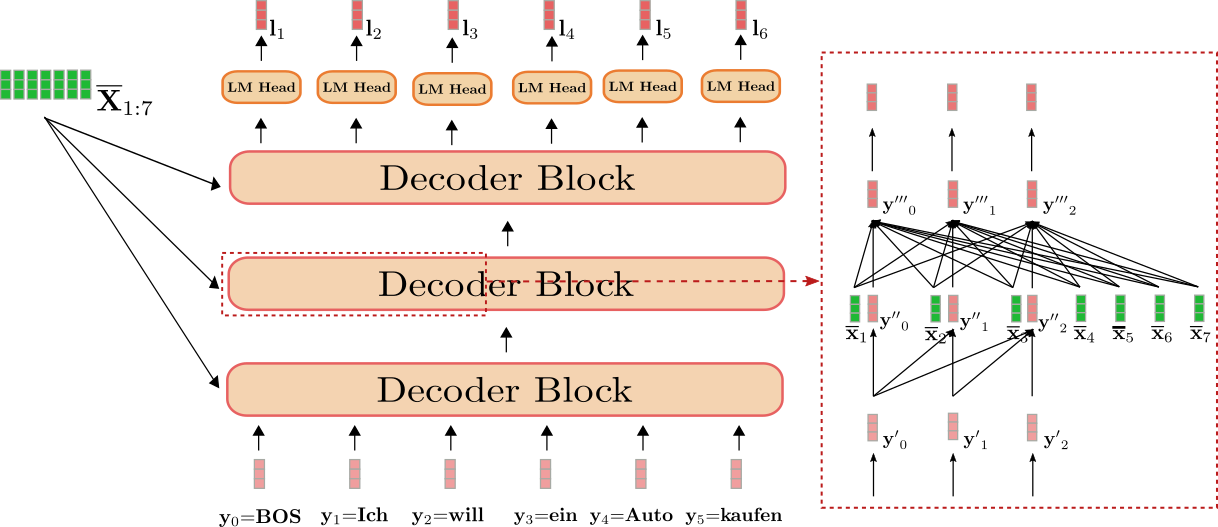
首先，讓我們瞭解一下基於 Transformer 的解碼器如何定義機率分佈。基於 Transformer 的解碼器是一堆*解碼器塊*，其後跟一個密集層，即“LM 頭”。解碼器塊堆疊將上下文化編碼序列 $\mathbf{\overline{X}}_{1:n}$ 和一個以 $\text{BOS}$ 向量為字首並截斷到最後一個目標向量的目標向量序列（即 $\mathbf{Y}_{0:i-1}$）對映到一個編碼的目標向量序列 $\mathbf{\overline{Y}}_{0: i-1}$。然後，“LM 頭”將編碼的目標向量序列 $\mathbf{\overline{Y}}_{0: i-1}$ 對映到一個 logit 向量序列 $\mathbf{L}_{1:n} = \mathbf{l}_1, \ldots, \mathbf{l}_n$，其中每個 logit 向量 $\mathbf{l}_i$ 的維度對應於詞彙表的大小。這樣，對於每個 $i \in \{1, \ldots, n\}$，透過對 $\mathbf{l}_i$ 應用 softmax 操作，可以獲得整個詞彙表的機率分佈。這些分佈定義了條件分佈

$$p_{\theta_{dec}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}), \forall i \in \{1, \ldots, n\},$$

。“LM 頭”通常與詞嵌入矩陣的轉置繫結，即 $\mathbf{W}_{\text{emb}}^{\intercal} = \left[\mathbf{y}^1, \ldots, \mathbf{y}^{\text{vocab}}\right]^{\intercal}$ ${}^1$。直觀地說，這意味著對於所有 $i \in \{0, \ldots, n - 1\}$，“LM 頭”層將編碼的輸出向量 $\mathbf{\overline{y}}_i$ 與詞彙表中的所有詞嵌入 $\mathbf{y}^1, \ldots, \mathbf{y}^{\text{vocab}}$ 進行比較，因此 logit 向量 $\mathbf{l}_{i+1}$ 表示編碼輸出向量與每個詞嵌入之間的相似度分數。softmax 操作只是將相似度分數轉換為機率分佈。對於每個 $i \in \{1, \ldots, n\}$，以下等式成立

$$p_{\theta_{dec}}(\mathbf{y} | \mathbf{\overline{X}}_{1:n}, \mathbf{Y}_{0:i-1})$$ $$= \text{Softmax}(f_{\theta_{\text{dec}}}(\mathbf{\overline{X}}_{1:n}, \mathbf{Y}_{0:i-1}))$$ $$= \text{Softmax}(\mathbf{W}_{\text{emb}}^{\intercal} \mathbf{\overline{y}}_{i-1})$$ $$= \text{Softmax}(\mathbf{l}_i).$$

總而言之，為了對目標向量序列 $\mathbf{Y}_{1: m}$ 的條件分佈進行建模，目標向量 $\mathbf{Y}_{1:m-1}$ 會前置一個特殊的 $\text{BOS}$ 向量，即 $\mathbf{y}_0$，然後首先與經過上下文處理的編碼序列 $\mathbf{\overline{X}}_{1:n}$ 一起對映到對數向量序列 $\mathbf{L}_{1:m}$。因此，每個對數目標向量 $\mathbf{l}_i$ 使用 softmax 操作被轉換為目標向量 $\mathbf{y}_i$ 的條件機率分佈。最後，所有目標向量 $\mathbf{y}_1, \ldots, \mathbf{y}_m$ 的條件機率相乘以得到完整目標向量序列的條件機率。

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} | \mathbf{\overline{X}}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{dec}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}).$$

與基於 transformer 的編碼器相比，在基於 transformer 的解碼器中，編碼後的輸出向量 $\mathbf{\overline{y}}_i$ 應該是對下一個目標向量 $\mathbf{y}_{i+1}$ 的良好表示，而不是對輸入向量本身的表示。此外，編碼後的輸出向量 $\mathbf{\overline{y}}_i$ 應該以所有經過上下文處理的編碼序列 $\mathbf{\overline{X}}_{1:n}$ 為條件。為滿足這些要求，每個解碼器塊都包含一個單向自注意力層，其後是一個交叉注意力層和兩個前饋層${}^2$。單向自注意力層僅將其每個輸入向量 $\mathbf{y'}_j$ 與所有先前的輸入向量 $\mathbf{y'}_i, \text{ with } i \le j$ 相關聯，以對所有 $j \in \{1, \ldots, n\}$ 的下一個目標向量的機率分佈進行建模。交叉注意力層將其每個輸入向量 $\mathbf{y''}_j$ 與所有經過上下文處理的編碼向量 $\mathbf{\overline{X}}_{1:n}$ 相關聯，從而也以編碼器的輸入為條件來確定下一個目標向量的機率分佈。

好的，讓我們為我們的英譯德翻譯示例將基於 transformer 的解碼器視覺化。

我們可以看到，解碼器將輸入 $\mathbf{Y}_{0:5}$ “BOS”、“Ich”、“will”、“ein”、“Auto”、“kaufen”（以淺紅色顯示）與 “I”、“want”、“to”、“buy”、“a”、“car”、“EOS” 的上下文序列（即 $\mathbf{\overline{X}}_{1:7}$，以深綠色顯示）一起對映到對數向量 $\mathbf{L}_{1:6}$（以深紅色顯示）。

對每個 $\mathbf{l}_1, \mathbf{l}_2, \ldots, \mathbf{l}_5$ 應用 softmax 操作，可以定義條件機率分佈

$$p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{\overline{X}}_{1:7}),$$ $$p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich}, \mathbf{\overline{X}}_{1:7}),$$ $$\ldots,$$ $$p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7}).$$

總的條件機率

$$p_{\theta_{dec}}(\text{Ich will ein Auto kaufen EOS} | \mathbf{\overline{X}}_{1:n})$$

因此可以計算為以下乘積

$$p_{\theta_{dec}}(\text{Ich} | \text{BOS}, \mathbf{\overline{X}}_{1:7}) \times \ldots \times p_{\theta_{dec}}(\text{EOS} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7}).$$

右邊的紅色方框顯示了前三個目標向量 $\mathbf{y}_0, \mathbf{y}_1, \mathbf{y}_2$ 的解碼器塊。下部展示了單向自注意力機制，中部展示了交叉注意力機制。讓我們首先關注單向自注意力。

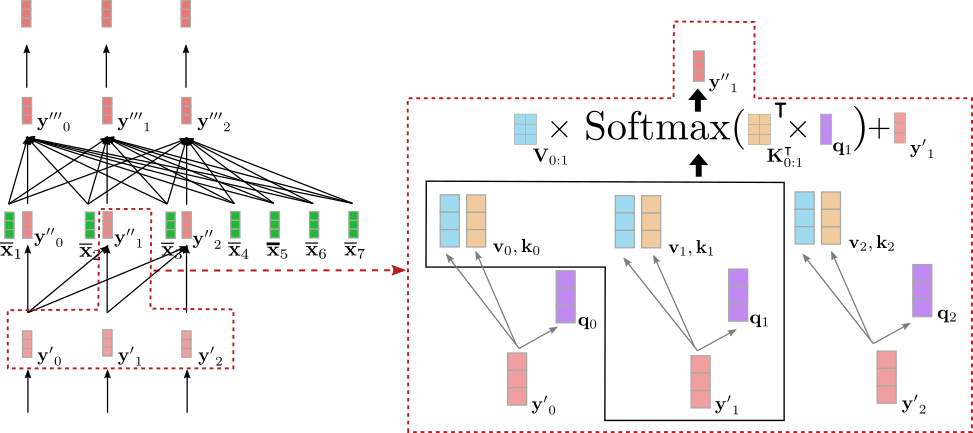
與雙向自注意力一樣，在單向自注意力中，查詢向量 $\mathbf{q}_0, \ldots, \mathbf{q}_{m-1}$（下圖紫色所示）、鍵向量 $\mathbf{k}_0, \ldots, \mathbf{k}_{m-1}$（下圖橙色所示）和值向量 $\mathbf{v}_0, \ldots, \mathbf{v}_{m-1}$（下圖藍色所示）都是從它們各自的輸入向量 $\mathbf{y'}_0, \ldots, \mathbf{y'}_{m-1}$（下圖淺紅色所示）投影得到的。然而，在單向自注意力中，每個查詢向量 $\mathbf{q}_i$僅與其各自的鍵向量和所有先前的鍵向量（即 $\mathbf{k}_0, \ldots, \mathbf{k}_i$）進行比較，以產生各自的注意力權重。這可以防止輸出向量 $\mathbf{y''}_j$（下圖深紅色所示）包含有關後續輸入向量 $\mathbf{y}_i, \text{ with } i > j$ 的任何資訊，其中 $j \in \{0, \ldots, m - 1 \}$。與雙向自注意力一樣，注意力權重隨後會與它們各自的值向量相乘並求和。

我們可以將單向自注意力總結如下

$$\mathbf{y''}_i = \mathbf{V}_{0: i} \textbf{Softmax}(\mathbf{K}_{0: i}^\intercal \mathbf{q}_i) + \mathbf{y'}_i.$$

請注意，鍵向量和值向量的索引範圍是 $0:i$ 而不是 $0: m-1$，後者是雙向自注意力中鍵向量的範圍。

讓我們為上面示例中的輸入向量 $\mathbf{y'}_1$ 演示一下單向自注意力。

可以看出，$\mathbf{y''}_1$僅取決於$\mathbf{y'}_0$和$\mathbf{y'}_1$。因此，我們將單詞“Ich”的向量表示，即$\mathbf{y'}_1$，僅與它自身和“BOS”目標向量（即$\mathbf{y'}_0$）建立關係，而不與單詞“will”的向量表示（即$\mathbf{y'}_2$）建立關係。

那麼，為什麼在解碼器中使用單向自注意力而不是雙向自注意力如此重要呢？如上所述，基於Transformer的解碼器定義了一個從輸入向量序列$\mathbf{Y}_{0: m-1}$到對應下一個解碼器輸入向量的對數（logits）的對映，即$\mathbf{L}_{1:m}$。在我們的例子中，這意味著，例如，輸入向量$\mathbf{y}_1$ = "Ich"被對映到對數向量$\mathbf{l}_2$，然後用於預測輸入向量$\mathbf{y}_2$。因此，如果$\mathbf{y'}_1$可以訪問後續的輸入向量$\mathbf{Y'}_{2:5}$，解碼器就會簡單地複製“will”的向量表示，即$\mathbf{y'}_2$，作為其輸出$\mathbf{y''}_1$。這將被前饋到最後一層，使得編碼後的輸出向量$\mathbf{\overline{y}}_1$基本上只對應於向量表示$\mathbf{y}_2$。

這顯然是不利的，因為基於Transformer的解碼器將永遠學不會根據之前所有的詞來預測下一個詞，而只是將目標向量$\mathbf{y}_i$透過網路複製到$\mathbf{\overline{y}}_{i-1}$，對於所有的$i \in \{1, \ldots, m \}$。為了定義下一個目標向量的條件分佈，該分佈不能以下一個目標向量本身為條件。從$p(\mathbf{y} | \mathbf{Y}_{0:i}, \mathbf{\overline{X}})$來預測$\mathbf{y}_i$是沒有意義的，因為這個分佈以它本應建模的目標向量為條件。因此，單向自注意力架構使我們能夠定義一個因果機率分佈，這對於有效地建模下一個目標向量的條件分佈是必要的。

太好了！現在我們可以轉向連線編碼器和解碼器的層——交叉注意力機制！

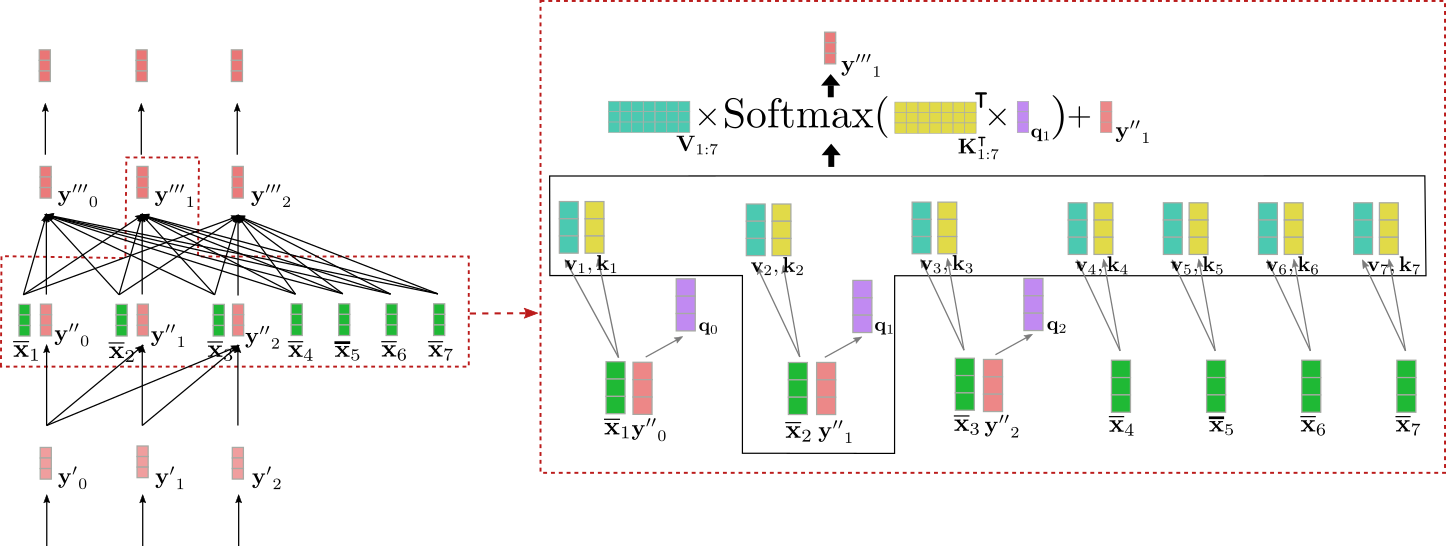
交叉注意力層接收兩個向量序列作為輸入：單向自注意力層的輸出，即$\mathbf{Y''}_{0: m-1}$，以及上下文編碼向量$\mathbf{\overline{X}}_{1:n}$。與自注意力層一樣，查詢向量$\mathbf{q}_0, \ldots, \mathbf{q}_{m-1}$是前一層輸出向量的投影，即$\mathbf{Y''}_{0: m-1}$。然而，鍵向量$\mathbf{k}_0, \ldots, \mathbf{k}_{m-1}$和值向量$\mathbf{v}_0, \ldots, \mathbf{v}_{m-1}$是上下文編碼向量$\mathbf{\overline{X}}_{1:n}$的投影。定義了鍵、值和查詢向量後，查詢向量$\mathbf{q}_i$會與所有鍵向量進行比較，相應的分數用於加權各自的值向量，就像雙向自注意力一樣，以得到輸出向量$\mathbf{y'''}_i$，對於所有的$i \in {0, \ldots, m-1}$。交叉注意力可以總結如下：

$$\mathbf{y'''}_i = \mathbf{V}_{1:n} \textbf{Softmax}(\mathbf{K}_{1: n}^\intercal \mathbf{q}_i) + \mathbf{y''}_i.$$

請注意，鍵和值向量的索引範圍是$1:n$，對應於上下文編碼向量的數量。

讓我們以上述示例中的輸入向量$\mathbf{y''}_1$為例，視覺化交叉注意力機制。

我們可以看到，查詢向量$\mathbf{q}_1$（紫色所示）源自$\mathbf{y''}_1$（紅色所示），因此它依賴於單詞“Ich”的向量表示。然後，查詢向量$\mathbf{q}_1$與鍵向量$\mathbf{k}_1, \ldots, \mathbf{k}_7$（黃色所示）進行比較，這些鍵向量對應所有編碼器輸入向量$\mathbf{X}_{1:n}$ = "I want to buy a car EOS"的上下文編碼表示。這將“Ich”的向量表示與所有編碼器輸入向量直接關聯起來。最後，注意力權重與值向量$\mathbf{v}_1, \ldots, \mathbf{v}_7$（綠松石色所示）相乘，除了輸入向量$\mathbf{y''}_1$之外，還得到輸出向量$\mathbf{y'''}_1$（深紅色所示）。

那麼，直觀上這裡到底發生了什麼？每個輸出向量$\mathbf{y'''}_i$是編碼器所有輸入值投影$\mathbf{v}_{1}, \ldots, \mathbf{v}_7$的加權和，再加上輸入向量本身$\mathbf{y''}_i$（參見上圖公式）。需要理解的關鍵機制如下：輸入解碼器向量的查詢投影$\mathbf{q}_i$與編碼器輸入向量的鍵投影$\mathbf{k}_j$的相似度越高，編碼器輸入向量的值投影$\mathbf{v}_j$就越重要。通俗地說，這意味著解碼器輸入表示與編碼器輸入表示越“相關”，該輸入表示對解碼器輸出表示的影響就越大。

酷！現在我們可以看到，該架構如何很好地將每個輸出向量 $\mathbf{y'''}_i$ 的生成條件，設定為編碼器輸入向量 $\mathbf{\overline{X}}_{1:n}$ 與輸入向量 $\mathbf{y''}_i$ 之間的互動。此時另一個重要的觀察是，該架構完全獨立於上下文編碼向量 $\mathbf{\overline{X}}_{1:n}$ 的數量 $n$，而輸出向量 $\mathbf{y'''}_i$ 的生成是以其為條件的。所有用於派生鍵向量 $\mathbf{k}_1, \ldots, \mathbf{k}_n$ 和值向量 $\mathbf{v}_1, \ldots, \mathbf{v}_n$ 的投影矩陣 $\mathbf{W}^{\text{cross}}_{k}$ 和 $\mathbf{W}^{\text{cross}}_{v}$ 在所有位置 $1, \ldots, n$ 之間共享，並且所有值向量 $\mathbf{v}_1, \ldots, \mathbf{v}_n$ 被求和為一個加權平均向量。現在，為什麼基於 Transformer 的解碼器不會遇到基於 RNN 的解碼器所面臨的長期依賴問題，也變得顯而易見了。因為每個解碼器 logit 向量都 *直接* 依賴於每個編碼輸出向量，所以比較第一個編碼輸出向量和最後一個解碼器 logit 向量所需的數學運算基本上只需要一步。

總而言之，單向自注意力層負責將每個輸出向量的生成條件，設定為所有先前的解碼器輸入向量和當前輸入向量；而交叉注意力層則負責進一步將每個輸出向量的生成條件，設定為所有編碼後的輸入向量。

為了驗證我們的理論理解，讓我們繼續上面編碼器部分的編碼示例。

---

${}^1$ 詞嵌入矩陣 $\mathbf{W}_{\text{emb}}$ 為每個輸入詞提供一個唯一的、*與上下文無關的* 向量表示。該矩陣通常被固定為“LM Head”層。然而，“LM Head”層完全可以由一個完全獨立的“編碼向量到 logit”的權重對映組成。

${}^2$ 同樣，詳細解釋前饋層在基於 Transformer 的模型中扮演的角色超出了本筆記的範圍。在 Yun 等人 (2017) 的論文中，他們認為前饋層對於將每個上下文向量 $\mathbf{x'}_i$ 單獨對映到所需的輸出空間至關重要，而*自注意力*層本身無法做到這一點。這裡需要注意的是，每個輸出詞元 $\mathbf{x'}$ 都由相同的前饋層處理。更多細節，建議讀者閱讀該論文。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")
embeddings = model.get_input_embeddings()

# create token ids for encoder input
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# pass input token ids to encoder
encoder_output_vectors = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state

# create token ids for decoder input
decoder_input_ids = tokenizer("<pad> Ich will ein", return_tensors="pt", add_special_tokens=False).input_ids

# pass decoder input ids and encoded input vectors to decoder
decoder_output_vectors = model.base_model.decoder(decoder_input_ids, encoder_hidden_states=encoder_output_vectors).last_hidden_state

# derive embeddings by multiplying decoder outputs with embedding weights
lm_logits = torch.nn.functional.linear(decoder_output_vectors, embeddings.weight, bias=model.final_logits_bias)

# change the decoder input slightly
decoder_input_ids_perturbed = tokenizer("<pad> Ich will das", return_tensors="pt", add_special_tokens=False).input_ids
decoder_output_vectors_perturbed = model.base_model.decoder(decoder_input_ids_perturbed, encoder_hidden_states=encoder_output_vectors).last_hidden_state
lm_logits_perturbed = torch.nn.functional.linear(decoder_output_vectors_perturbed, embeddings.weight, bias=model.final_logits_bias)

# compare shape and encoding of first vector
print(f"Shape of decoder input vectors {embeddings(decoder_input_ids).shape}. Shape of decoder logits {lm_logits.shape}")

# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `Ich` equal to its perturbed version?: ", torch.allclose(lm_logits[0, 0], lm_logits_perturbed[0, 0], atol=1e-3))

輸出

    Shape of decoder input vectors torch.Size([1, 5, 512]). Shape of decoder logits torch.Size([1, 5, 58101])
    Is encoding for `Ich` equal to its perturbed version?:  True

我們將解碼器輸入詞嵌入的輸出形狀，即 `embeddings(decoder_input_ids)`（對應於 $\mathbf{Y}_{0: 4}$，這裡 `<pad>` 對應於 BOS，“Ich will das” 被分詞為 4 個詞元）與 `lm_logits` 的維度（對應於 $\mathbf{L}_{1:5}$）進行比較。此外，我們還將詞序列“`<pad>` Ich will ein”和稍微擾動過的版本“`<pad>` Ich will das”與 `encoder_output_vectors` 一起傳遞給解碼器，以檢查當輸入序列中只有最後一個詞被改變時（“ein” -> “das”），第二個 `lm_logit`（對應於“Ich”）是否會不同。

正如預期的那樣，解碼器輸入詞嵌入和 lm_logits 的輸出形狀，即 $\mathbf{Y}_{0: 4}$ 和 $\mathbf{L}_{1:5}$ 的維度在最後一個維度上是不同的。雖然序列長度相同（=5），但解碼器輸入詞嵌入的維度對應於 `model.config.hidden_size`，而 `lm_logit` 的維度對應於詞彙表大小 `model.config.vocab_size`，如上所述。其次，可以注意到，當最後一個詞從“ein”變為“das”時，$\mathbf{l}_1 = \text{"Ich"}$ 的編碼輸出向量的值是相同的。然而，如果理解了單向自注意力，這應該不足為奇。

最後，順便提一下，像 GPT2 這樣的 *自迴歸* 模型，其架構與基於 *Transformer* 的解碼器模型相同，**前提是** 去掉交叉注意力層，因為獨立的自迴歸模型不依賴任何編碼器輸出。所以自迴歸模型本質上與 *自編碼* 模型相同，只是用單向注意力取代了雙向注意力。這些模型也可以在海量開放域文字資料上進行預訓練，以在自然語言生成（NLG）任務上展現出令人印象深刻的效能。在 Radford 等人 (2019) 的論文中，作者們展示了一個預訓練的 GPT2 模型可以在各種 NLG 任務上取得 SOTA 或接近 SOTA 的結果，而無需太多微調。所有 🤗Transformers 的 *自迴歸* 模型都可以在這裡找到。

好了，就是這樣！現在，您應該對基於 *Transformer* 的編碼器-解碼器模型以及如何使用 🤗Transformers 庫有了很好的理解。

非常感謝 Victor Sanh、Sasha Rush、Sam Shleifer、Oliver Åstrand、‪Ted Moskovitz 和 Kristian Kyvik 提供了寶貴的反饋。

附錄

如上所述，以下程式碼片段展示瞭如何為基於 *Transformer* 的編碼器-解碼器模型編寫一個簡單的生成方法。在這裡，我們使用 `torch.argmax` 實現了一種簡單的 *貪心* 解碼方法來對目標向量進行取樣。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# create BOS token
decoder_input_ids = tokenizer("<pad>", add_special_tokens=False, return_tensors="pt").input_ids

assert decoder_input_ids[0, 0].item() == model.config.decoder_start_token_id, "`decoder_input_ids` should correspond to `model.config.decoder_start_token_id`"

# STEP 1

# pass input_ids to encoder and to decoder and pass BOS token to decoder to retrieve first logit
outputs = model(input_ids, decoder_input_ids=decoder_input_ids, return_dict=True)

# get encoded sequence
encoded_sequence = (outputs.encoder_last_hidden_state,)
# get logits
lm_logits = outputs.logits

# sample last token with highest prob
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)

# concat
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# STEP 2

# reuse encoded_inputs and pass BOS + "Ich" to decoder to second logit
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits

# sample last token with highest prob again
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)

# concat again
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# STEP 3
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# let's see what we have generated so far!
print(f"Generated so far: {tokenizer.decode(decoder_input_ids[0], skip_special_tokens=True)}")

# This can be written in a loop as well.

輸出

    Generated so far: Ich will ein

在這個程式碼示例中，我們展示的正是前面描述的內容。我們將輸入“I want to buy a car”與 $\text{BOS}$ 詞元一起傳遞給編碼器-解碼器模型，並從第一個 logit $\mathbf{l}_1$（即 `lm_logits` 的第一行）進行取樣。在這裡，我們的取樣策略很簡單：貪心地選擇機率最高的下一個解碼器輸入向量。然後，我們以自迴歸的方式，將取樣到的解碼器輸入向量與之前的輸入一起傳遞給編碼器-解碼器模型，並再次取樣。我們重複這個過程第三次。結果，模型生成了“Ich will ein”這幾個詞。結果非常準確——這是輸入正確翻譯的開頭部分。

在實踐中，會使用更復雜的解碼方法來對 `lm_logits` 進行取樣。其中大部分方法都在這篇部落格文章中有所介紹。