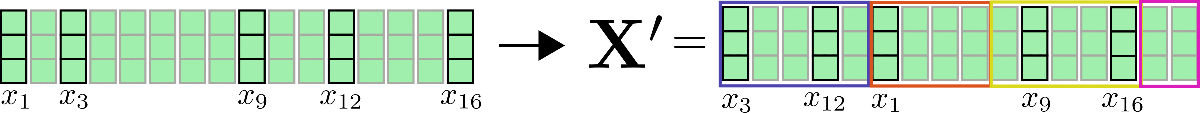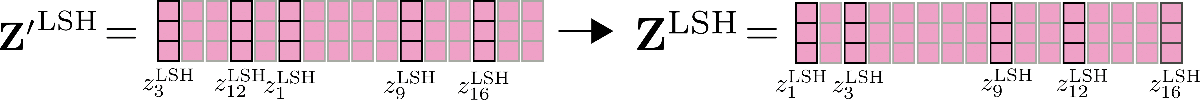Reformer——突破語言模型限制

Patrick von Platen

patrickvonplaten

關注

Reformer 如何使用不到 8GB 記憶體訓練 50 萬個詞元的序列

由 Kitaev、Kaiser 等人 (2020) 提出的 Reformer 模型是目前用於長序列建模的最節省記憶體的 Transformer 模型之一。

最近，長序列建模引起了廣泛關注，僅今年就有許多相關提交，例如 Beltagy 等人 (2020)、Roy 等人 (2020)、Tay 等人、Wang 等人。長序列建模的動機是，NLP 中的許多工，例如摘要、問答，要求模型處理比 BERT 等模型能夠處理的更長的輸入序列。在需要模型處理大型輸入序列的任務中，長序列模型無需截斷輸入序列以避免記憶體溢位，因此已被證明優於標準“BERT”類模型，參見 Beltagy 等人 (2020)。

Reformer 透過其一次處理多達 50 萬個詞元的能力（如本演示所示），將長序列建模的極限推向了新的高度。相比之下，傳統的 bert-base-uncased 模型將輸入長度限制為僅 512 個詞元。在 Reformer 中，標準 Transformer 架構的每個部分都經過重新設計，以最佳化最小記憶體需求，同時效能沒有顯著下降。

記憶體改進可歸因於 Reformer 作者引入 Transformer 領域的 4 個特性

1. Reformer 自注意力層 - 如何在不受本地上下文限制的情況下高效實現自注意力？
2. 分塊前饋層 - 如何為大型前饋層獲得更好的時間-記憶體權衡？
3. 可逆殘差層 - 如何透過巧妙的殘差架構大幅減少訓練中的記憶體消耗？
4. 軸向位置編碼 - 如何使位置編碼適用於極長輸入序列？

本部落格文章的目標是讓讀者深入瞭解上述四個 Reformer 特性。雖然解釋側重於 Reformer，但讀者應該能更好地理解這四個特性在何種情況下對其他 Transformer 模型也有效。這四個部分之間只有鬆散的聯絡，因此可以獨立閱讀。

Reformer 是 🤗Transformers 庫的一部分。對於所有 Reformer 使用者，建議仔細閱讀這篇非常詳細的部落格文章，以便更好地理解模型的工作原理以及如何正確設定其配置。所有公式都附有其在 Reformer 配置中的等效名稱，例如 config.，以便讀者可以快速查閱官方文件和配置檔案。

注意：官方 Reformer 論文中沒有解釋軸向位置編碼，但它們在官方程式碼庫中被廣泛使用。本部落格文章首次深入解釋了軸向位置編碼。

1. Reformer 自注意力層

Reformer 使用兩種特殊的自注意力層：區域性自注意力層和區域性敏感雜湊 (LSH) 自注意力層。

為了更好地介紹這些新的自注意力層，我們將簡要回顧 Vaswani 等人 2017 中介紹的傳統自注意力。

本部落格文章使用與流行部落格文章 The illustrated transformer 相同的符號和顏色，因此強烈建議讀者首先閱讀該部落格。

重要：Reformer 最初是為因果自注意力引入的，但它也可以很好地用於雙向自注意力。在這篇文章中，Reformer 的自注意力以雙向自注意力的形式呈現。

全域性自注意力回顧

每個 Transformer 模型的核心是自注意力層。為了回顧傳統的自注意力層（這裡我們稱之為全域性自注意力層），我們假設將 Transformer 層應用於嵌入向量序列 $\mathbf{X} = \mathbf{x}_1, \ldots, \mathbf{x}_n$，其中每個向量 $\mathbf{x}_{i}$ 的大小為 config.hidden_size，即 $d_h$。

簡而言之，全域性自注意力層將 $\mathbf{X}$ 投影到查詢、鍵和值矩陣 $\mathbf{Q}, \mathbf{K}, \mathbf{V}$，並使用 softmax 運算計算輸出 $\mathbf{Z}$，如下所示：$\mathbf{Z} = \text{SelfAttn}(\mathbf{X}) = \text{softmax}(\mathbf{Q}\mathbf{K}^T) \mathbf{V}$，其中 $\mathbf{Z}$ 的維度為 $d_h \times n$（為簡化起見，省略了鍵歸一化因子和自注意力權重 $\mathbf{W}^{O}$）。有關完整 Transformer 操作的更多詳細資訊，請參閱 The illustrated transformer。

在視覺化方面，我們可以將此操作說明如下，其中 $n=16, d_h=3$

請注意，對於所有視覺化，batch_size 和 config.num_attention_heads 都假定為 1。某些向量，例如 $\mathbf{x_3}$ 及其對應的輸出向量 $\mathbf{z_3}$ 被標記，以便稍後更好地解釋 LSH 自注意力。所呈現的邏輯可以毫不費力地擴充套件到多頭自注意力（config.num_attention_{h}eads > 1）。建議讀者閱讀 The illustrated transformer 作為多頭自注意力的參考。

重要的是要記住，對於每個輸出向量 $\mathbf{z}_{i}$，處理了整個輸入序列 $\mathbf{X}$。內積 $\mathbf{Q}\mathbf{K}^T$ 張量的漸近記憶體複雜度為 $\mathcal{O}(n^2)$，這通常是 Transformer 模型中的記憶體瓶頸。

這也是 bert-base-cased 的 config.max_position_embedding_size 僅為 512 的原因。

區域性自注意力

區域性自注意力是減少 $\mathcal{O}(n^2)$ 記憶體瓶頸的顯而易見的解決方案，它允許我們以降低的計算成本對更長的序列進行建模。在區域性自注意力中，輸入 $\mathbf{X} = \mathbf{X}_{1:n} = \mathbf{x}_{1}, \ldots, \mathbf{x}_{n}$ 被切成 $n_{c}$ 個塊：$\mathbf{X} = \left[\mathbf{X}_{1:l_{c}}, \ldots, \mathbf{X}_{(n_{c} - 1) * l_{c} : n_{c} * l_{c}}\right]$，每個塊的長度為 config.local_chunk_length，即 $l_{c}$，然後對每個塊分別應用全域性自注意力。

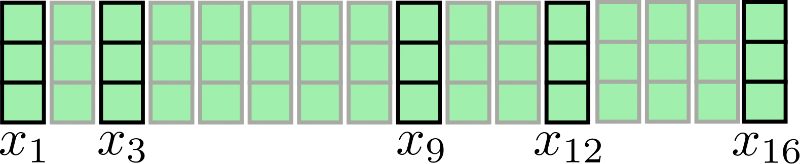
讓我們再次以 $n=16, d_h=3$ 的輸入序列為例進行視覺化

假設 $l_{c} = 4, n_{c} = 4$4，分塊注意力可以視覺化如下

正如所見，注意力操作分別應用於每個塊 $\mathbf{X}_{1:4}, \mathbf{X}_{5:8}, \mathbf{X}_{9:12}, \mathbf{X}_{13:16}$。這種架構的第一個缺點顯而易見：某些輸入向量無法訪問其直接上下文，例如在我們的示例中，$\mathbf{x}_9$ 無法訪問 $\mathbf{x}_{8}$，反之亦然。這很成問題，因為這些詞元無法學習考慮到其直接上下文的詞表示。

一個簡單的補救措施是為每個塊增加 config.local_num_chunks_before，即 $n_{p}$ 個塊，以及 config.local_num_chunks_after，即 $n_{a}$ 個塊，這樣每個輸入向量至少可以訪問 $n_{p}$ 個先前的輸入向量和 $n_{a}$ 個後續輸入向量。這也可以理解為具有重疊的分塊，其中 $n_{p}$ 和 $n_{a}$ 定義了每個塊與所有先前塊和後續塊的重疊量。我們將這種擴充套件的區域性自注意力表示為

$$\mathbf{Z}^{\text{loc}} = \left[\mathbf{Z}_{1:l_{c}}^{\text{loc}}, \ldots, \mathbf{Z}_{(n_{c} - 1) * l_{c} : n_{c} * l_{c}}^{\text{loc}}\right],$$loc​], 其中 $$\mathbf{Z}_{l_{c} * (i - 1) + 1 : l_{c} * i}^{\text{loc}} = \text{SelfAttn}(\mathbf{X}_{l_{c} * (i - 1 - n_{p}) + 1: l_{c} * (i + n_{a})})\left[n_{p} * l_{c}: -n_{a} * l_{c}\right], \forall i \in \{1, \ldots, n_{c} \}$$=SelfAttn(Xlc​∗(i−1−np​)+1:lc​∗(i+na​)​)[np​∗lc​:−na​∗lc​],∀i∈{1,…,nc​}

好的，這個公式看起來很複雜。讓我們簡化它。在 Reformer 的自注意力層中，$n_{a}$ 通常設定為 0，$n_{p}$ 設定為 1，因此讓我們再次寫下 $i = 1$ 的公式

$$\mathbf{Z}_{1:l_{c}}^{\text{loc}} = \text{SelfAttn}(\mathbf{X}_{-l_{c} + 1: l_{c}})\left[l_{c}:\right]$$=SelfAttn(X−lc​+1:lc​​)[lc​:]

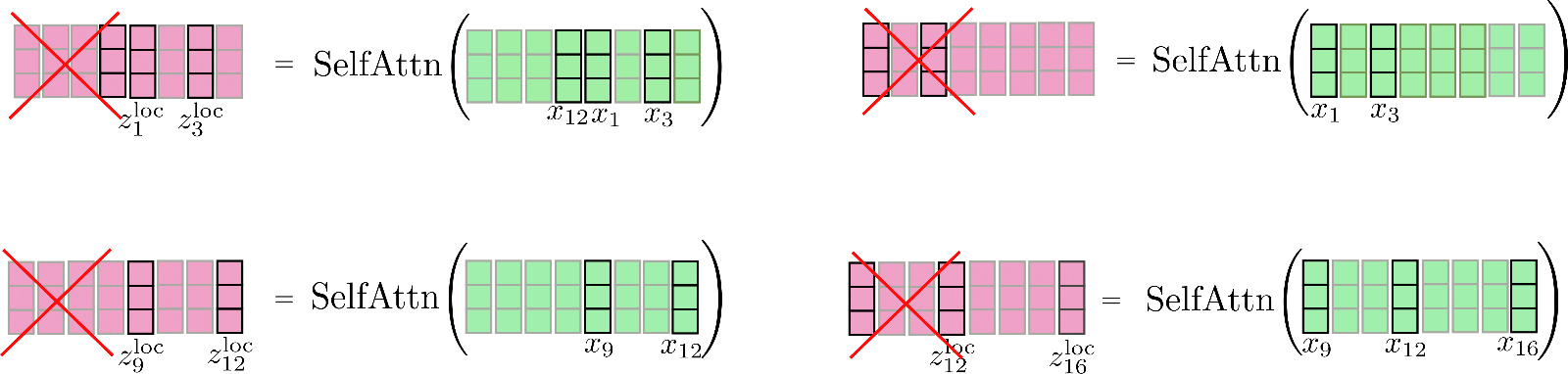
我們注意到存在迴圈關係，因此第一個段也可以關注最後一個段。讓我們再次說明這種略微增強的區域性注意力。首先，我們在每個視窗化段內應用自注意力，並只保留中心輸出段。

最後，將相關輸出連線到 $\mathbf{Z}^{\text{loc}}$，其結果如下所示。

請注意，區域性自注意力是以高效方式實現的，因此不會像此處為說明目的而用紅叉表示的那樣計算並隨後“丟棄”任何輸出。

這裡需要注意的是，擴充套件每個分塊自注意力函式的輸入向量可以使每個單一輸出向量$\mathbf{z}_{i}$更好地學習向量表示。例如，輸出向量$\mathbf{z}_{5}^{\text{loc}}, \mathbf{z}_{6}^{\text{loc}}, \mathbf{z}_{7}^{\text{loc}}, \mathbf{z}_{8}^{\text{loc}}$都可以考慮所有輸入向量$\mathbf{X}_{1:8}$來學習更好的表示。

記憶體消耗的增長顯而易見：$\mathcal{O}(n^2)$的記憶體複雜度被分解為每個段單獨處理，從而將總漸近記憶體消耗降低到$\mathcal{O}(n_{c} * l_{c}^2) = \mathcal{O}(n * l_{c})$。

這種增強的區域性自注意力優於普通的區域性自注意力架構，但仍然存在一個主要缺點，即每個輸入向量只能關注預定義大小的區域性上下文。對於不需要Transformer模型學習輸入向量之間長距離依賴關係的NLP任務（其中可能包括語音識別、命名實體識別和短句子因果語言建模），這可能不是一個大問題。許多NLP任務確實需要模型學習長距離依賴關係，因此區域性自注意力可能導致顯著的效能下降，例如：

• 問答：模型必須學習問題標記和相關答案標記之間的關係，這些標記很可能不在同一個區域性範圍內。
• 多項選擇：模型必須比較多個答案標記段，這些段通常由顯著的長度分隔。
• 摘要：模型必須學習長序列上下文標記和短序列摘要標記之間的關係，而上下文和摘要之間的相關關係很可能無法透過區域性自注意力捕獲。
• 等等...

區域性自注意力本身很可能不足以讓Transformer模型學習輸入向量（標記）之間的相關關係。

因此，Reformer還採用了近似全域性自注意力的有效自注意力層，稱為LSH自注意力。

LSH自注意力

好了，既然我們已經瞭解了局部自注意力是如何工作的，我們就可以嘗試Reformer中最具創新性的部分：區域性敏感雜湊（LSH）自注意力。

LSH自注意力前提是效率或多或少與區域性自注意力相當，同時近似全域性自注意力。

LSH自注意力依賴於Andoni等人（2015）中提出的LSH演算法，因此得名。

LSH自注意力的思想基於一個洞察力：如果$n$很大，則應用於$\mathbf{Q}\mathbf{K}^T$注意力點積權重上的softmax函式對於每個查詢向量只有少數值明顯大於0。

我們來詳細解釋一下。設$\mathbf{k}_{i} \in \mathbf{K} = \left[\mathbf{k}_1, \ldots, \mathbf{k}_n \right]^T$和$\mathbf{q}_{i} \in \mathbf{Q} = \left[\mathbf{q}_1, \ldots, \mathbf{q}_n\right]^T$為鍵向量和查詢向量。對於每個$\mathbf{q}_{i}$，計算$\text{softmax}(\mathbf{q}_{i}^T \mathbf{K}^T)$可以透過僅使用與$\mathbf{q}_{i}$具有高餘弦相似度的鍵向量$\mathbf{k}_{j}$來近似。這是因為softmax函式對較大的輸入值賦予指數級更多的權重。到目前為止一切順利，下一個問題是高效地找到與所有$i$的$\mathbf{q}_{i}$具有高餘弦相似度的向量。

首先，Reformer的作者注意到共享查詢和鍵投影：$\mathbf{Q} = \mathbf{K}$不會影響Transformer模型的效能${}^1$。現在，不再需要為每個查詢向量$q_i$查詢具有高餘弦相似度的鍵向量，只需要找到查詢向量彼此之間的餘弦相似度。這很重要，因為查詢-查詢向量點積近似具有傳遞性：如果$\mathbf{q}_{i}$與查詢向量$\mathbf{q}_{j}$和$\mathbf{q}_{k}$具有高餘弦相似度，那麼$\mathbf{q}_{j}$也與$\mathbf{q}_{k}$具有高餘弦相似度。因此，查詢向量可以被聚類到桶中，使得屬於同一桶的所有查詢向量彼此之間具有高餘弦相似度。我們定義$C_{m}$為第m組位置索引，使得其對應的查詢向量在同一桶中：$C_{m} = \{ i | \text{ s.t. } \mathbf{q}_{i} \in \text{mth cluster}\}$和config.num_buckets，即$n_{b}$，為桶的數量。

對於每組索引$C_{m}$，在相應查詢向量桶上的softmax函式$\text{softmax}(\mathbf{Q}_{i \in C_{m}} \mathbf{Q}^T_{i \in C_{m}})$近似了共享查詢和鍵投影的全域性自注意力函式$\text{softmax}(\mathbf{q}_{i}^T \mathbf{Q}^T)$，適用於$C_{m}$中所有位置索引$i$。

其次，作者利用LSH演算法將查詢向量聚類到預定義數量的桶$n_{b}$中。LSH演算法是理想的選擇，因為它非常高效，並且是餘弦相似度最近鄰演算法的近似。本筆記本不討論LSH方案，因此我們只需記住，對於每個向量$\mathbf{q}_{i}$，LSH演算法將其位置索引$i$歸因於$n_{b}$個預定義桶中的一個，即$\text{LSH}(\mathbf{q}_{i}) = m$，其中$i \in \{1, \ldots, n\}$和$m \in \{1, \ldots, n_{b}\}$。

在視覺上，我們可以用我們的原始示例來闡述這一點：

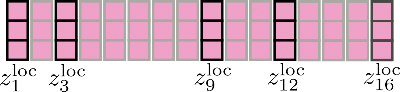
第三，需要注意的是，在將所有查詢向量聚類到$n_{b}$個桶中之後，相應的索引集$C_{m}$可以用來相應地置換輸入向量$\mathbf{x}_1, \ldots, \mathbf{x}_n$${}^2$，以便可以像區域性注意力一樣分段應用共享查詢鍵自注意力。

我們再用我們的示例輸入向量$\mathbf{X} = \mathbf{x}_1, ..., \mathbf{x}_{16}$進行闡述，假設config.num_buckets=4和config.lsh_chunk_length = 4。看上面的圖，我們可以看到我們已經將每個查詢向量$\mathbf{q}_1, \ldots, \mathbf{q}_{16}$分配到其中一個叢集$\mathcal{C}_{1}, \mathcal{C}_{2}, \mathcal{C}_{3}, \mathcal{C}_{4}$。如果現在我們將相應的輸入向量$\mathbf{x}_1, \ldots, \mathbf{x}_{16}$進行排序，我們將得到以下置換後的輸入$\mathbf{X'}$

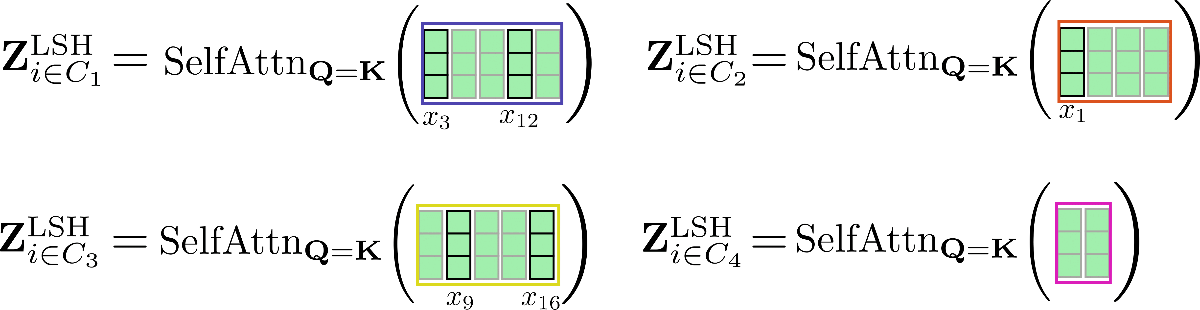
自注意力機制應該獨立地應用於每個叢集，以便對於每個叢集$\mathcal{C}_m$，其相應的輸出計算如下：$\mathbf{Z}^{\text{LSH}}_{i \in \mathcal{C}_m} = \text{SelfAttn}_{\mathbf{Q}=\mathbf{K}}(\mathbf{X}_{i \in \mathcal{C}_m})$。

我們再用這個例子來解釋一下。

可以看出，自注意力函式操作於不同大小的矩陣，這對於GPU和TPU中的高效批處理來說並不理想。

為了解決這個問題，可以像區域性注意力一樣對置換後的輸入進行分塊，使得每個塊的大小為config.lsh_chunk_length。透過對置換後的輸入進行分塊，一個桶可能會被分成兩個不同的塊。為了解決這個問題，在LSH自注意力中，每個塊除了關注自身之外，還會關注其前一個塊config.lsh_num_chunks_before=1，這與區域性自注意力的方式相同（config.lsh_num_chunks_after通常設定為0）。透過這種方式，我們可以確保一個桶中的所有向量以高機率相互關注${}^3$。

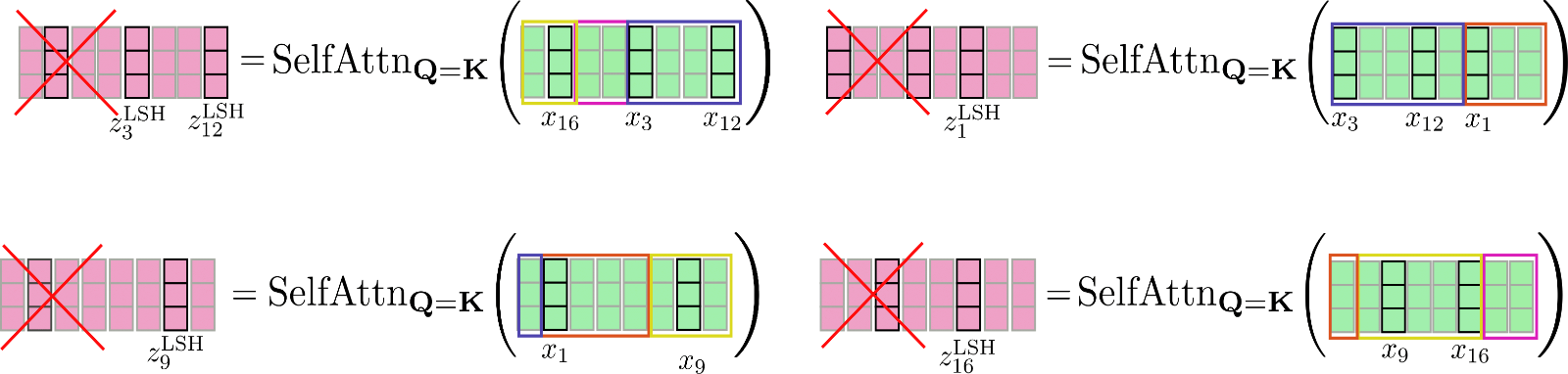
總而言之，對於所有塊$k \in \{1, \ldots, n_{c}\}$，LSH自注意力可以記作如下

$$\mathbf{Z'}_{l_{c} * k + 1:l_{c} * (k + 1)}^{\text{LSH}} = \text{SelfAttn}_{\mathbf{Q} = \mathbf{K}}(\mathbf{X'}_{l_{c} * k + 1): l_{c} * (k + 1)})\left[l_{c}:\right]$$

其中 $\mathbf{X'}$ 和 $\mathbf{Z'}$ 是根據 LSH 演算法排列的輸入和輸出向量。公式太複雜了，我們來演示一下 LSH 自注意力機制。

如上所示，排列後的向量 $\mathbf{X'}$ 被分塊，並且共享查詢鍵的自注意力機制被應用於每個塊。

最後，輸出 $\mathbf{Z'}^{\text{LSH}}$ 被重新排序為原始排列。

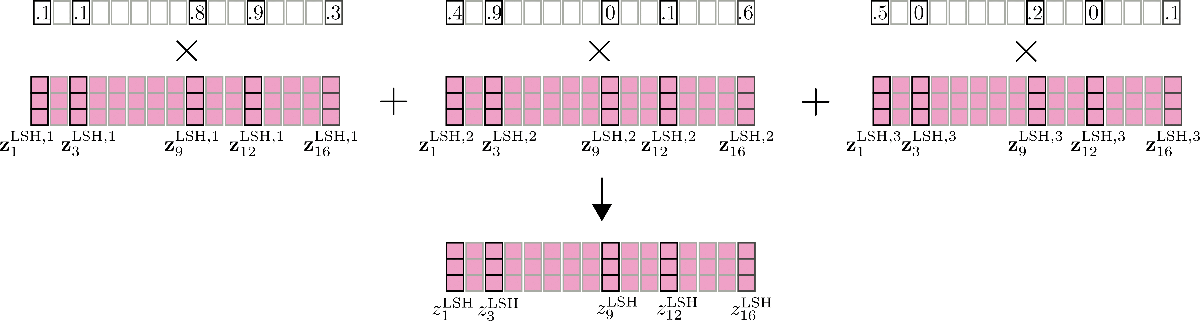
這裡還要提到一個重要特性：LSH 自注意力的準確性可以透過並行執行 LSH 自注意力 `config.num_hashes` 次（例如 $n_{h}$ 次），每次使用不同的隨機 LSH 雜湊來提高。透過設定 `config.num_hashes > 1`，對於每個輸出位置 $i$，計算並隨後合併多個輸出向量：$\mathbf{z}^{\text{LSH}, 1}_{i}, \ldots, \mathbf{z}^{\text{LSH}, n_{h}}_{i}$，然後合併：$\mathbf{z}^{\text{LSH}}_{i} = \sum_k^{n_{h}} \mathbf{Z}^{\text{LSH}, k}_{i} * \text{weight}^k_i$。其中 $\text{weight}^k_i$ 表示雜湊輪次 $k$ 的輸出向量 $\mathbf{z}^{\text{LSH}, k}_{i}$ 相對於其他雜湊輪次的重要性，並且與它們的 softmax 計算的歸一化項呈指數比例。這背後的直覺是，如果相應的查詢向量 $\mathbf{q}_{i}^{k}$ 與其所在塊中的所有其他查詢向量具有高度的餘弦相似性，那麼該塊的 softmax 歸一化項往往會很高，因此相應的輸出向量 $\mathbf{q}_{i}^{k}$ 應該能更好地近似全域性注意力，因此比 softmax 歸一化項較低的雜湊輪次的輸出向量獲得更多權重。更多詳情請參閱論文附錄 A。對於我們的示例，多輪 LSH 自注意力可以如下所示。

太棒了。就是這樣。現在我們知道 Reformer 中 LSH 自注意力是如何工作的了。

關於記憶體複雜度，我們現在有兩個術語相互競爭，成為記憶體瓶頸：點積：$\mathcal{O}(n_{h} * n_{c} * l_{c}^2) = \mathcal{O}(n * n_{h} * l_{c})$ 和 LSH 分桶所需的記憶體：$\mathcal{O}(n * n_{h} * \frac{n_{b}}{2})$，其中 $l_{c}$ 是塊長度。因為對於大的 $n$，桶的數量 $\frac{n_{b}}{2}$ 比塊長度 $l_{c}$ 增長得更快，使用者可以再次對桶的數量 `config.num_buckets` 進行因式分解，如此處所述。

讓我們快速回顧一下上面所講的內容

1. 我們希望利用 softmax 操作僅將顯著權重分配給極少數鍵向量的知識來近似全域性注意力。
2. 如果鍵向量等於查詢向量，這意味著*對於每個*查詢向量 $\mathbf{q}_{i}$，softmax 只會將顯著權重分配給在餘弦相似度方面相似的其他查詢向量。
3. 這種關係是雙向的，這意味著如果 $\mathbf{q}_{j}$ 與 $\mathbf{q}_{i}$ 相似，那麼 $\mathbf{q}_{j}$ 也與 $\mathbf{q}_{i}$ 相似，因此我們可以在對排列的輸入應用自注意力之前進行全域性聚類。
4. 我們將區域性自注意力應用於排列後的輸入，然後將輸出重新排序為原始排列。

${}^{1}$ 作者進行了一些初步實驗，證實共享查詢鍵自注意力與標準自注意力表現或多或少一樣好。

${}^{2}$ 更準確地說，桶內的查詢向量根據其原始順序進行排序。這意味著如果，*例如*，向量 $\mathbf{q}_1, \mathbf{q}_3, \mathbf{q}_7$,q7​ 都被雜湊到桶 2，那麼桶 2 中向量的順序仍然是 $\mathbf{q}_1$，然後是 $\mathbf{q}_3$ 和 $\mathbf{q}_7$。

${}^3$ 另外值得一提的是，作者對查詢向量 $\mathbf{q}_{i}$ 進行了掩碼處理，以防止向量注意自身。因為向量與自身的餘弦相似度總是高於或等於與其他向量的餘弦相似度，所以在共享查詢鍵自注意力中，強烈不鼓勵查詢向量注意自身。

基準測試

基準測試工具最近已新增到 Transformers 中 - 詳情請參閱此處。

為了展示使用“區域性”+“LSH”自注意力可以節省多少記憶體，Reformer 模型 `google/reformer-enwik8` 在不同的 `local_attn_chunk_length` 和 `lsh_attn_chunk_length` 下進行了基準測試。`google/reformer-enwik8` 模型的預設配置和用法可以在此處檢視更多詳情。

首先，讓我們進行一些必要的匯入和安裝。

#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml

from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments

首先，讓我們使用*全域性*自注意力來測試 Reformer 模型的記憶體使用情況。這可以透過設定 `lsh_attn_chunk_length` = `local_attn_chunk_length` = 8192 來實現，這樣對於所有小於或等於 8192 的輸入序列，模型會自動切換到全域性自注意力。

config = ReformerConfig.from_pretrained("google/reformer-enwik8", lsh_attn_chunk_length=16386, local_attn_chunk_length=16386, lsh_num_chunks_before=0, local_num_chunks_before=0)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[2048, 4096, 8192, 16386], batch_sizes=[1], models=["Reformer"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config], args=benchmark_args)
result = benchmark.run()

HBox(children=(FloatProgress(value=0.0, description='Downloading', max=1279.0, style=ProgressStyle(description…



1 / 1
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 8.87 GiB already allocated; 1.92 GiB free; 8.88 GiB reserved in total by PyTorch)

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
           Reformer                  1              2048            1465     
           Reformer                  1              4096            2757     
           Reformer                  1              8192            7893     
           Reformer                  1             16386            N/A      
--------------------------------------------------------------------------------

輸入序列越長，輸入序列與峰值記憶體使用量之間的二次關係 $\mathcal{O}(n^2)$ 就越明顯。可以看出，實際上需要更長的輸入序列才能清楚地觀察到輸入序列翻倍，峰值記憶體使用量就會翻兩番。

對於使用全域性注意力的 `google/reformer-enwik8` 模型，序列長度超過 16K 會導致記憶體溢位。

現在，讓我們透過使用模型的預設引數來啟用*區域性*和*LSH*自注意力。

  config = ReformerConfig.from_pretrained("google/reformer-enwik8")
  benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[2048, 4096, 8192, 16384, 32768, 65436], batch_sizes=[1], models=["Reformer"], no_speed=True, no_env_print=True)
  benchmark = PyTorchBenchmark(configs=[config], args=benchmark_args)
  result = benchmark.run()

1 / 1
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 7.85 GiB already allocated; 1.74 GiB free; 9.06 GiB reserved in total by PyTorch)
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 4.00 GiB (GPU 0; 11.17 GiB total capacity; 6.56 GiB already allocated; 3.99 GiB free; 6.81 GiB reserved in total by PyTorch)

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
           Reformer                  1              2048            1785     
           Reformer                  1              4096            2621     
           Reformer                  1              8192            4281     
           Reformer                  1             16384            7607     
           Reformer                  1             32768            N/A      
           Reformer                  1             65436            N/A      
--------------------------------------------------------------------------------

正如所料，使用區域性和 LSH 自注意力對於較長的輸入序列來說效率更高，因此在該筆記本中，模型僅在 16K 令牌的 11GB RAM GPU 上才耗盡記憶體。

2. 分塊前饋層

基於 Transformer 的模型通常在自注意力層之後並行使用非常大的前饋層。因此，該層會佔用大量總記憶體，有時甚至成為模型的記憶體瓶頸。前饋分塊技術首次在 Reformer 論文中提出，它允許有效地權衡更好的記憶體消耗與增加的時間消耗。

Reformer 中的分塊前饋層

在 Reformer 中，*LSH* 或*區域性*自注意力層通常後接殘差連線，這便定義了*Transformer 塊*的第一部分。有關此內容的更多詳細資訊，請參閱此部落格。

*Transformer 塊*第一部分的輸出，稱為*規範化自注意力*輸出，可以寫為 $\mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X}$，其中 $\mathbf{Z}$ 要麼是 Reformer 中的 $\mathbf{Z}^{\text{LSH}}$，要麼是 $\mathbf{Z}^\text{loc}$。

對於我們的示例輸入 $\mathbf{x}_1, \ldots, \mathbf{x}_{16}$，我們如下所示地說明規範化自注意力輸出。

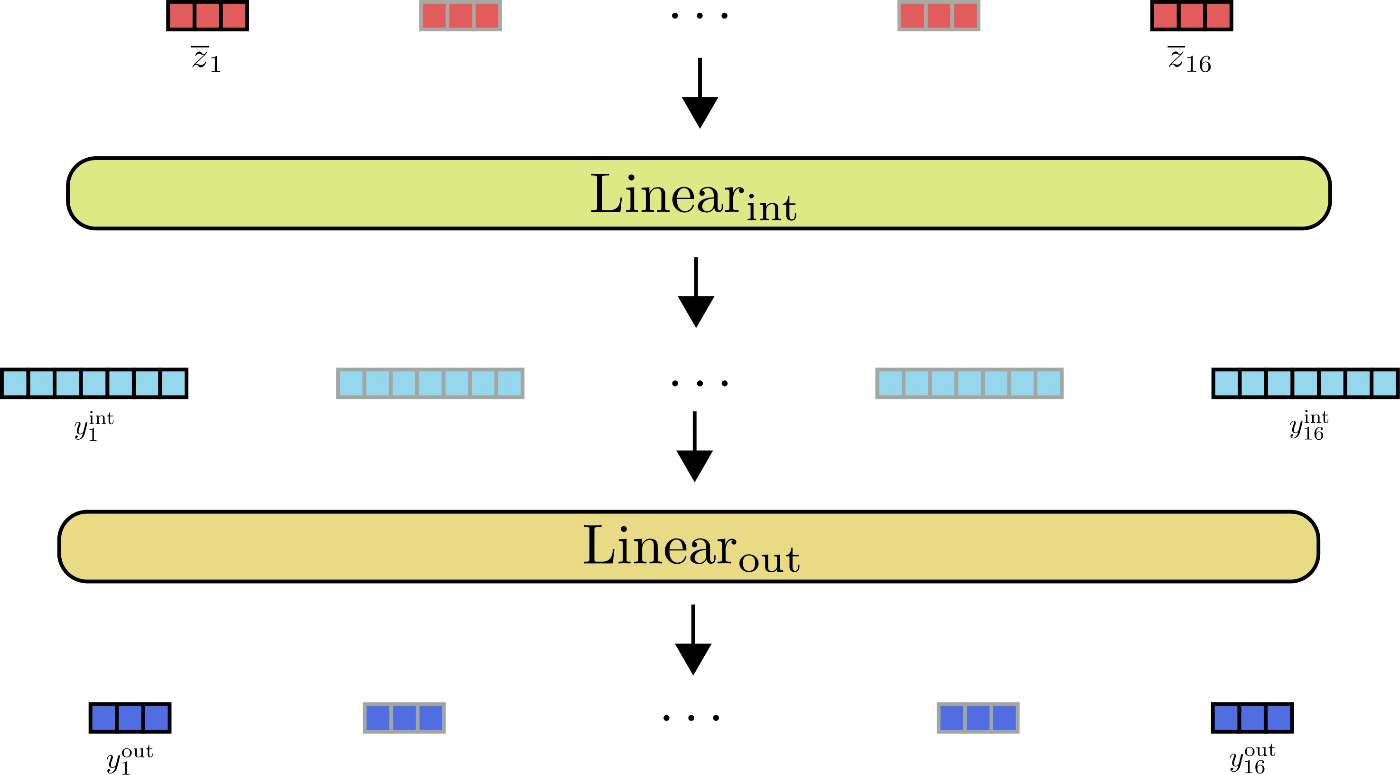
現在，*Transformer 塊*的第二部分通常由兩個前饋層 $^{1}$ 組成，定義為 $\text{Linear}_{\text{int}}(\ldots)$，用於處理 $\mathbf{\overline{Z}}$，得到中間輸出 $\mathbf{Y}_{\text{int}}$ 和 $\text{Linear}_{\text{out}}(\ldots)$，用於處理中間輸出，得到輸出 $\mathbf{Y}_{\text{out}}$。這兩個前饋層可以定義為

$$\mathbf{Y}_{\text{out}} = \text{Linear}_{\text{out}}(\mathbf{Y}_\text{int}) = \text{Linear}_{\text{out}}(\text{Linear}_{\text{int}}(\mathbf{\overline{Z}})).$$

此時重要的是要記住，從數學上講，前饋層在位置 $\mathbf{y}_{\text{out}, i}$ 的輸出僅取決於此位置的輸入 $\mathbf{\overline{y}}_{i}$。與自注意力層不同，每個輸出 $\mathbf{y}_{\text{out}, i}$ 完全獨立於不同位置的所有輸入 $\mathbf{\overline{y}}_{j \ne i}$。

讓我們為 $\mathbf{\overline{z}}_1, \ldots, \mathbf{\overline{z}}_{16}$ 說明前饋層。

從圖中可以看出，所有輸入向量 $\mathbf{\overline{z}}_{i}$ 都由相同的前饋層並行處理。

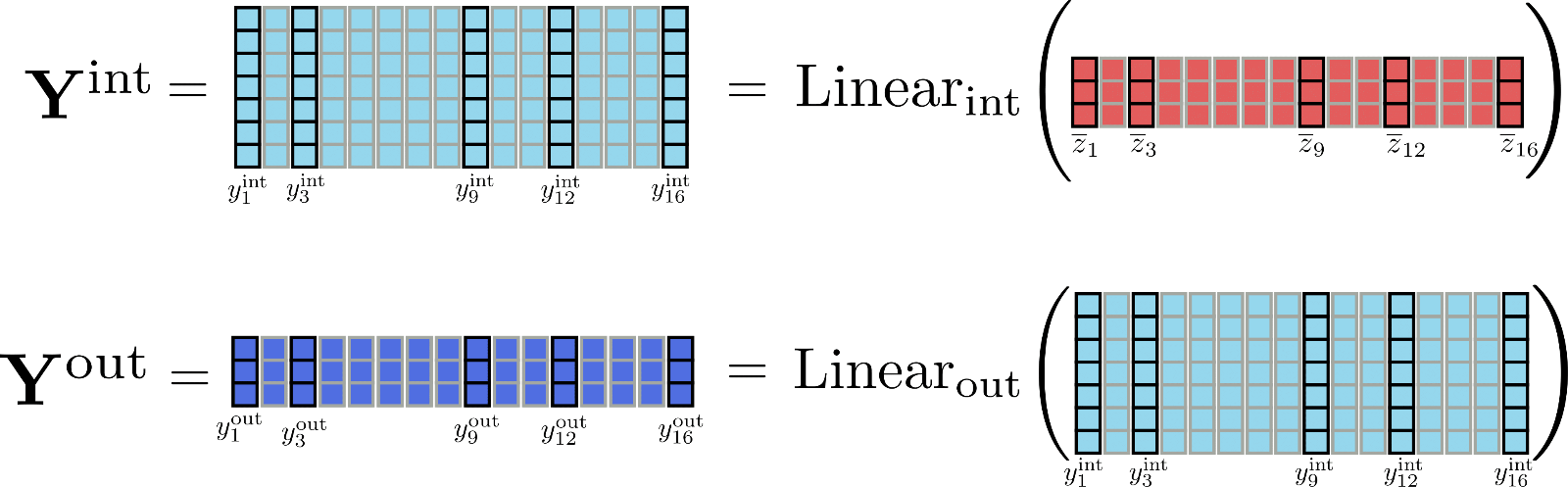
當我們檢視前饋層的輸出維度時，會變得有趣。在 Reformer 中，$\text{Linear}_{\text{int}}$ 的輸出維度定義為 config.feed_forward_size，例如 $d_{f}$，而 $\text{Linear}_{\text{out}}$ 的輸出維度定義為 config.hidden_size，即 $d_{h}$。

Reformer 的作者觀察到，在 Transformer 模型中，中間維度 $d_{f}$ 通常遠大於輸出維度 $^{2}$ $d_{h}$。這意味著維度為 $d_{f} \times n$ 的張量 $\mathbf{\mathbf{Y}}_\text{int}$ 分配了總記憶體的很大一部分，甚至可能成為記憶體瓶頸。

為了更好地理解維度差異，我們以示例為例，描繪矩陣 $\mathbf{Y}_\text{int}$ 和 $\mathbf{Y}_\text{out}$。

很明顯，張量 $\mathbf{Y}_\text{int}$ 佔用記憶體要大得多（確切地說，是 $\frac{d_{f}}{d_{h}} \times n$ 倍）比 $\mathbf{Y}_{\text{out}}$ 大。但是，是否真的有必要計算完整的中間矩陣 $\mathbf{Y}_\text{int}$ 呢？並非如此，因為相關的只有輸出矩陣 $\mathbf{Y}_\text{out}$。因此，為了用記憶體換取速度，可以將線性層的計算分塊，一次只處理一個塊。將 config.chunk_size_feed_forward 定義為 $c_{f}$，分塊線性層定義為 $\mathbf{Y}_{\text{out}} = \left[\mathbf{Y}_{\text{out}, 1: c_{f}}, \ldots, \mathbf{Y}_{\text{out}, (n - c_{f}): n}\right]$，其中 $\mathbf{Y}_{\text{out}, (c_{f} * i): (i * c_{f} + i)} = \text{Linear}_{\text{out}}(\text{Linear}_{\text{int}}(\mathbf{\overline{Z}}_{(c_{f} * i): (i * c_{f} + i)}))$。實際上，這僅意味著輸出是逐步計算並連線起來的，以避免在記憶體中儲存整個中間張量 $\mathbf{Y}_{\text{int}}$。

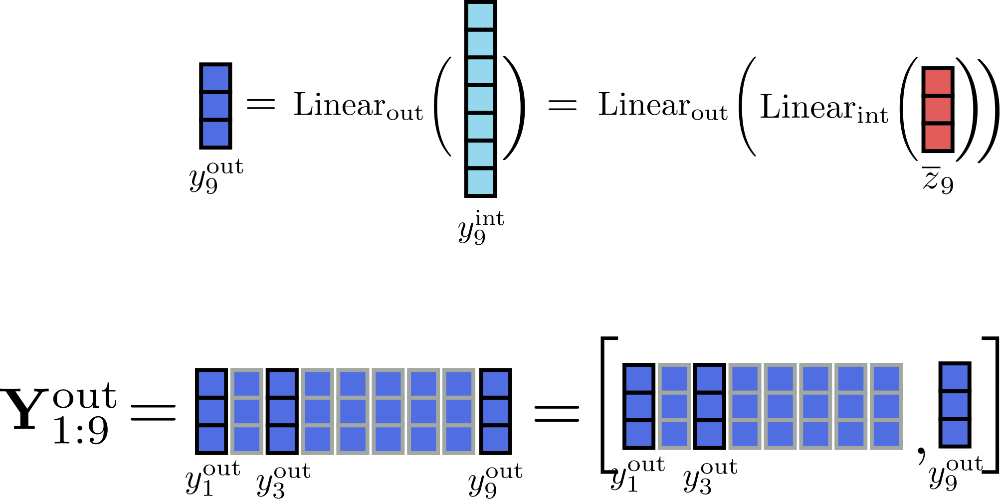
假設我們的示例中 $c_{f}=1$，我們可以如下所示說明位置 $i=9$ 的輸出的增量計算。

透過以大小為 1 的塊處理輸入，唯一需要同時儲存在記憶體中的張量是最大大小為 $16 \times d_{h}$ 的 $\mathbf{Y}_\text{out}$，大小為 $d_{f}$ 的 $\mathbf{y}_{\text{int}, i}$ 和大小為 $16 \times d_{h}$ 的輸入 $\mathbf{\overline{Z}}$，其中 $d_{h}$ 是 config.hidden_size $^{3}$。

最後，重要的是要記住，**分塊線性層**產生的輸出在數學上等同於傳統的線性層，因此可以應用於所有 Transformer 線性層。因此，利用 config.chunk_size_feed_forward 可以在某些使用場景下實現記憶體和速度之間更好的權衡。

${}^1$ 為了更簡單的解釋，通常在被前饋層處理之前應用於 $\mathbf{\overline{Z}}$ 的層歸一化層暫時省略。

${}^2$ 例如，在 bert-base-uncased 中，中間維度 $d_{f}$ 為 3072，是輸出維度 $d_{h}$ 的四倍。

${}^3$ 提醒一下，為了清晰和說明，本筆記本中假設輸出 config.num_attention_heads 為 1，因此自注意力層的輸出可以假定為 config.hidden_size 大小。

有關分塊線性/前饋層的更多資訊，也可以在 🤗Transformers 文件的此處找到。

基準測試

#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml

from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments

  Building wheel for transformers (setup.py) ... [?25l[?25hdone

config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8")  # no chunk
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1)  # feed forward chunk
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()

1 / 2
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 7.85 GiB already allocated; 1.74 GiB free; 9.06 GiB reserved in total by PyTorch)
2 / 2
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 7.85 GiB already allocated; 1.24 GiB free; 9.56 GiB reserved in total by PyTorch)

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
      Reformer-No-Chunk              8              1024            4281     
      Reformer-No-Chunk              8              2048            7607     
      Reformer-No-Chunk              8              4096            N/A      
        Reformer-Chunk               8              1024            4309     
        Reformer-Chunk               8              2048            7669     
        Reformer-Chunk               8              4096            N/A      
--------------------------------------------------------------------------------

config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=0, num_attention_{h}eads=2, feed_forward_size=16384)  # no chuck
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1, num_attention_{h}eads=2, feed_forward_size=16384)  # feed forward chunk
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()

1 / 2
2 / 2

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
      Reformer-No-Chunk              8              1024            3743     
      Reformer-No-Chunk              8              2048            5539     
      Reformer-No-Chunk              8              4096            9087     
        Reformer-Chunk               8              1024            2973     
        Reformer-Chunk               8              2048            3999     
        Reformer-Chunk               8              4096            6011     
--------------------------------------------------------------------------------

3. 可逆殘差層

可逆殘差層最初由N. Gomez 等人提出，用於在訓練流行的 *ResNet* 模型時減少記憶體消耗。在數學上，可逆殘差層與“真正”的殘差層略有不同，但不需要在正向傳播期間儲存啟用，這可以顯著減少訓練期間的記憶體消耗。

Reformer 中的可逆殘差層

讓我們首先探討為什麼訓練模型比模型推理需要更多的記憶體。

在模型推理時，所需的記憶體或多或少等於模型中**單個**最大張量所需的記憶體。另一方面，在訓練模型時，所需的記憶體或多或少等於所有可微分張量的**總和**。

考慮到深度學習框架中自動微分的工作方式，這並不奇怪。多倫多大學 Roger Grosse 的這些講座幻燈片對於更好地理解自動微分很有幫助。

簡而言之，為了計算可微分函式（例如，一個層）的梯度，自動微分需要函式的輸出梯度以及函式的輸入和輸出張量。雖然梯度是動態計算並隨後丟棄的，但函式的輸入和輸出張量（也稱為啟用）在正向傳播期間被儲存。

好的，讓我們將其應用於 Transformer 模型。Transformer 模型包含多個所謂的 Transformer 層堆疊。每個額外的 Transformer 層都強制模型在正向傳播期間儲存更多的啟用，從而增加訓練所需的記憶體。讓我們仔細看看。Transformer 層本質上由兩個殘差層組成。第一個殘差層表示第 1 節中解釋的 *自注意力* 機制，第二個殘差層表示第 2 節中解釋的 *線性* 或前饋層。

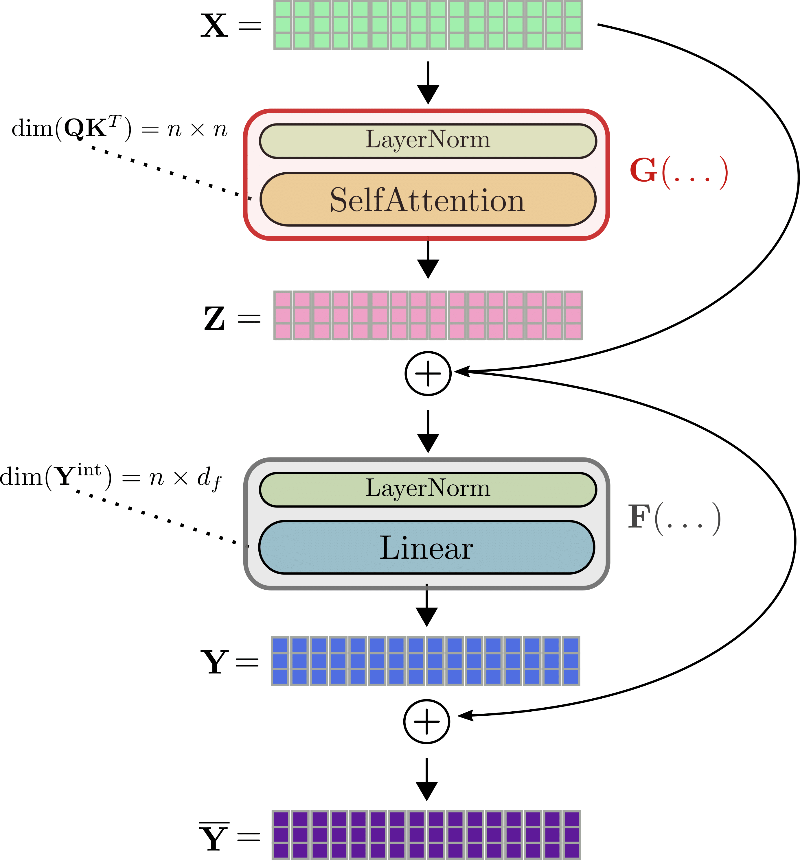
使用與之前相同的符號，Transformer 層的輸入，即 $\mathbf{X}$，首先被歸一化 $^{1}$，然後由自注意力層處理以獲得輸出 $\mathbf{Z} = \text{SelfAttn}(\text{LayerNorm}(\mathbf{X}))$。我們將這兩個層縮寫為 $G$，因此 $\mathbf{Z} = G(\mathbf{X})$。接下來，殘差 $\mathbf{Z}$ 被新增到輸入 $\mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X}$，並將總和輸入到第二個殘差層——兩個線性層。$\mathbf{\overline{Z}}$ 由第二個歸一化層處理，然後是兩個線性層，得到 $\mathbf{Y} = \text{Linear}(\text{LayerNorm}(\mathbf{Z} + \mathbf{X}))$。我們將第二個歸一化層和兩個線性層縮寫為 $F$，得到 $\mathbf{Y} = F(\mathbf{\overline{Z}})$。最後，殘差 $\mathbf{Y}$ 被新增到 $\mathbf{\overline{Z}}$，從而得到 Transformer 層的輸出 $\mathbf{\overline{Y}} = \mathbf{Y} + \mathbf{\overline{Z}}$。

讓我們以 $\mathbf{x}_1, \ldots, \mathbf{x}_{16}$ 為例，說明一個完整的 Transformer 層。

為了計算例如自注意力塊 $G$ 的梯度，需要提前知道三個張量：梯度 $\partial \mathbf{Z}$、輸出 $\mathbf{Z}$ 和輸入 $\mathbf{X}$。雖然 $\partial \mathbf{Z}$ 可以即時計算並隨後丟棄，但 $\mathbf{Z}$ 和 $\mathbf{X}$ 的值必須在正向傳播期間計算和儲存，因為在反向傳播期間無法輕鬆即時重新計算它們。因此，在正向傳播期間，大型張量輸出，例如查詢-鍵點積矩陣 $\mathbf{Q}\mathbf{K}^T$ 或線性層的中間輸出 $\mathbf{Y}^{\text{int}}$，必須儲存在記憶體中 $^{2}$。

在這裡，可逆殘差層就派上用場了。其思想相對簡單。殘差塊的設計方式是，無需儲存函式的輸入和輸出張量，而是在反向傳播期間可以輕鬆地重新計算兩者，這樣在正向傳播期間就無需在記憶體中儲存任何張量。這是透過使用兩個輸入流 $\mathbf{X}^{(1)}, \mathbf{X}^{(2)}$ 和兩個輸出流 $\mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)}$ 實現的。第一個殘差 $\mathbf{Z}$ 由第一個輸出流計算，即 $\mathbf{Z} = G(\mathbf{X}^{(1)})$，並隨後新增到第二個輸入流的輸入中，使得 $\mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X}^{(2)}$。同樣，殘差 $\mathbf{Y} = F(\mathbf{\overline{Z}})$ 再次新增到第一個輸入流中，因此兩個輸出流定義為 $\mathbf{Y}^{(1)} = \mathbf{Y} + \mathbf{X}^{(1)}$ 和 $\mathbf{Y}^{(2)} = \mathbf{X}^{(2)} + \mathbf{Z} = \mathbf{\overline{Z}}$。

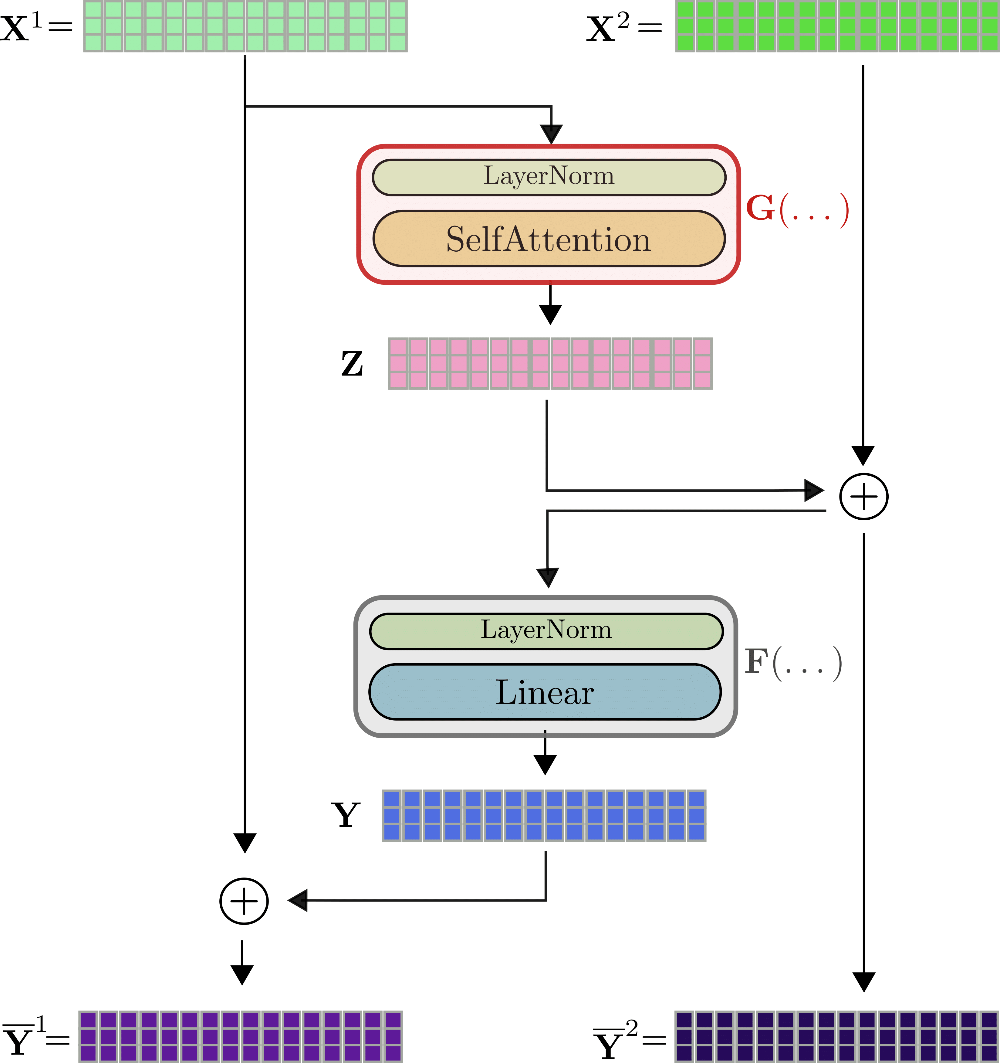
可逆Transformer層可進行視覺化，例如$\mathbf{x}_1, \ldots, \mathbf{x}_{16}$，如下所示。

可以看出，輸出$\mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)}$的計算方式與不可逆層中的$\mathbf{\overline{Y}}$非常相似，但它們在數學上是不同的。Reformer的作者在一些初步實驗中觀察到，可逆Transformer模型的效能與標準Transformer模型的效能相匹配。與標準Transformer層的第一個顯著區別是，它有兩個輸入流和兩個輸出流$^{3}$，這最初會稍微增加前向傳播所需的記憶體。然而，雙流架構對於前向傳播過程中無需儲存任何啟用是至關重要的。我們來解釋一下。對於反向傳播，可逆Transformer層需要計算梯度$\partial G$和$\partial F$。除了可以即時計算的梯度$\partial \mathbf{Y}$和$\partial \mathbf{Z}$之外，為了使自動微分生效，還需要知道$\partial F$的張量值$\mathbf{Y}$、$\mathbf{\overline{Z}}$，以及$\partial G$的張量值$\mathbf{Z}$和$\mathbf{X}^{(1)}$。

如果我們假設已知$\mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)}$，那麼從圖中很容易看出，可以如下計算$\mathbf{X}^{(1)}, \mathbf{X}^{(2)}$。$\mathbf{X}^{(1)} = F(\mathbf{\overline{Y}}^{(1)}) - \mathbf{\overline{Y}}^{(1)}$。很好，既然$\mathbf{X}^{(1)}$已知，$\mathbf{X}^{(2)}$可以透過$\mathbf{X}^{(2)} = \mathbf{\overline{Y}}^{(1)} - G(\mathbf{X}^{(1)})$計算。現在，$\mathbf{Z}$和$\mathbf{Y}$透過$\mathbf{Y} = \mathbf{\overline{Y}}^{(1)} - \mathbf{X}^{(1)}$和$\mathbf{Z} = \mathbf{\overline{Y}}^{(2)} - \mathbf{X}^{(2)}$可輕鬆計算。因此，結論是，如果在前向傳播過程中僅儲存**最後一個**可逆Transformer層的輸出$\mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)}$，那麼所有其他相關啟用都可以透過在反向傳播過程中利用$G$和$F$並傳遞$\mathbf{X}^{(1)}$和$\mathbf{X}^{(2)}$來推導。在反向傳播過程中，每個可逆Transformer層G和F的兩次前向傳播開銷，換取了前向傳播過程中無需儲存任何啟用的優勢。這是一個不錯的權衡！

注：最近，主要的深度學習框架已經發布了程式碼，允許僅儲存某些啟用，並在反向傳播期間重新計算較大的啟用（Tensorflow 此處和PyTorch 此處）。對於標準可逆層，這仍然意味著每個Transformer層至少需要儲存一個啟用，但透過定義哪些啟用可以動態重新計算，可以節省大量記憶體。

$^{1}$ 在前兩節中，我們省略了自注意力層和線性層之前的層歸一化層。讀者應該知道，$\mathbf{X}$和$\mathbf{\overline{Z}}$在分別送入自注意力層和線性層之前，都經過了層歸一化處理。$^{2}$ 儘管在設計中$\mathbf{Q}\mathbf{K}$的維度寫為$n \times n$，但在*LSH自注意力*或*區域性自注意力*層中，維度僅為$n \times l_{c} \times n_{h}$或$n \times l_{c}$，其中$l_{c}$是塊長度，$n_{h}$是雜湊數量。$^{3}$ 在第一個可逆Transformer層中，$\mathbf{X}^{(2)}$設定為等於$\mathbf{X}^{(1)}$。

基準測試

為了衡量可逆殘差層的影響，我們將比較BERT與Reformer在訓練過程中隨著層數增加的記憶體消耗。

#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml

from transformers import ReformerConfig, BertConfig, PyTorchBenchmark, PyTorchBenchmarkArguments

讓我們透過將層數從4增加到12來測量標準bert-base-uncased BERT模型所需的記憶體。

config_4_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=4)
config_8_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=8)
config_12_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=12)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Bert-4-Layers", "Bert-8-Layers", "Bert-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_bert, config_8_layers_bert, config_12_layers_bert], args=benchmark_args)
result = benchmark.run()

HBox(children=(FloatProgress(value=0.0, description='Downloading', max=433.0, style=ProgressStyle(description_…



1 / 3
2 / 3
3 / 3

====================        TRAIN - MEMORY - RESULTS        ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
        Bert-4-Layers                8              512             4103     
        Bert-8-Layers                8              512             5759     
        Bert-12-Layers               8              512             7415     
--------------------------------------------------------------------------------

可以看出，增加一層BERT會使所需記憶體線性增加超過400MB。

config_4_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=4, num_hashes=1)
config_8_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=8, num_hashes=1)
config_12_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=12, num_hashes=1)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-4-Layers", "Reformer-8-Layers", "Reformer-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_reformer, config_8_layers_reformer, config_12_layers_reformer], args=benchmark_args)
result = benchmark.run()

1 / 3
2 / 3
3 / 3

====================        TRAIN - MEMORY - RESULTS        ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
      Reformer-4-Layers              8              512             4607     
      Reformer-8-Layers              8              512             4987     
      Reformer-12-Layers             8              512             5367     
--------------------------------------------------------------------------------

另一方面，對於Reformer，在實踐中，增加一層所需的記憶體會顯著減少。增加一層平均會使所需記憶體增加不到100MB，因此一個更大的12層reformer-enwik8模型所需的記憶體比一個12層bert-base-uncased模型要少。

4. 軸向位置編碼

Reformer使得處理巨大的輸入序列成為可能。然而，對於如此長的輸入序列，僅標準位置編碼權重矩陣就會佔用超過1GB的記憶體來儲存其權重。為了防止如此大的位置編碼矩陣，官方Reformer程式碼引入了*軸向位置編碼*。

重要提示：*軸向位置編碼未在官方論文中解釋，但可以透過檢視程式碼並與作者交流來很好地理解*

Reformer中的軸向位置編碼

Transformer需要位置編碼來解釋輸入中單詞的順序，因為自注意力層*沒有順序概念*。位置編碼通常由一個簡單的查詢矩陣$\mathbf{E} = \left[\mathbf{e}_1, \ldots, \mathbf{e}_{n_\text{max}}\right]$定義。然後，位置編碼向量$\mathbf{e}_{i}$簡單地新增到第*i*個輸入向量$\mathbf{x}_{i} + \mathbf{e}_{i}$上，這樣模型就可以區分輸入向量（也稱為token）是在位置$i$還是$j$。對於每個輸入位置，模型需要能夠查詢對應的位置編碼向量，因此$\mathbf{E}$的維度由模型可以處理的最大輸入向量長度config.max_position_embeddings（即$n_\text{max}$）和輸入向量的config.hidden_size（即$d_{h}$）定義。

假設$d_{h}=4$且$n_\text{max}=49$，這樣的位置編碼矩陣可以如下視覺化

這裡，我們僅展示了維度（即高度）為4的位置編碼$\mathbf{e}_{1}$、$\mathbf{e}_{2}$和$\mathbf{e}_{49}$。

假設我們希望訓練一個Reformer模型，其序列長度可達0.5M個token，輸入向量的`config.hidden_size`為1024（參見此處的notebook）。相應的位置嵌入大小為$0.5M \times 1024 \sim 512M$個引數，這相當於2GB的大小。

這樣的位置編碼在模型載入到記憶體和儲存到硬碟時都會佔用不必要的巨大記憶體量。

Reformer 的作者透過將 `config.hidden_size` 維度一分為二，並巧妙地將 $n_\text{max}$ 維度因子分解，從而大幅縮小了位置編碼的尺寸。在 Transformer 中，使用者可以透過將 `config.axial_pos_shape` 設定為兩個適當的值 $n_\text{max}^1$ 和 $n_\text{max}^2$ 來決定 $n_\text{max}$ 可以分解成的形狀，從而滿足 $n_\text{max}^1 \times n_\text{max}^2 = n_\text{max}$。透過將 `config.axial_pos_embds_dim` 設定為兩個適當的值 $d_{h}^{1}$ 和 $d_{h}^2$，從而滿足 $d_{h}^1 + d_{h}^2 = d_{h}$，使用者可以決定隱藏維度如何被切割。現在，讓我們更直觀地進行視覺化和解釋。

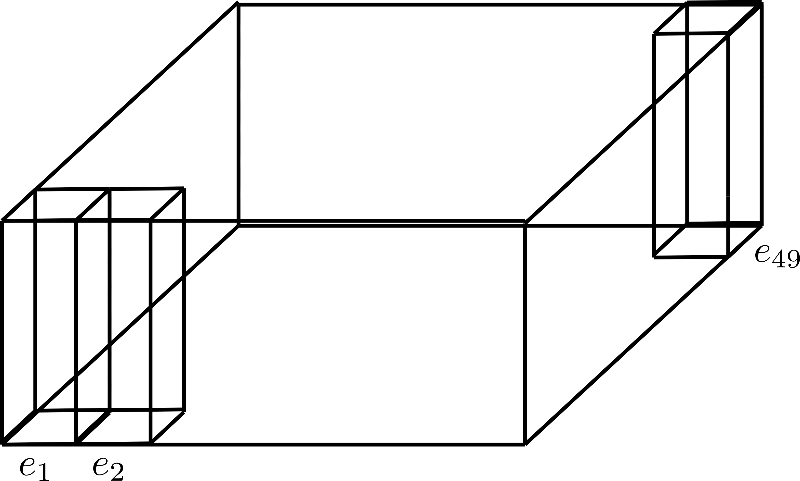
可以將$n_{\text{max}}$的因子分解想象成將維度摺疊成第三個軸，這在以下`config.axial_pos_shape = [7, 7]`的因子分解中顯示出來

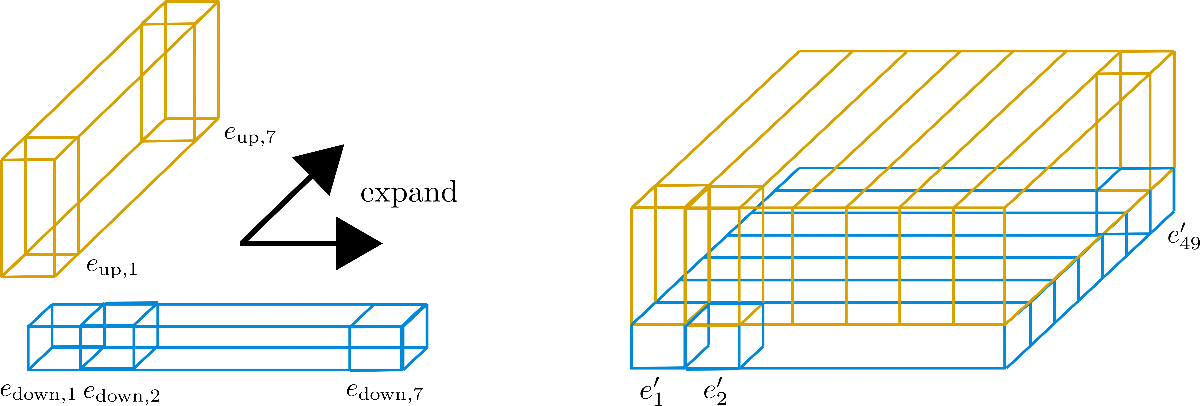
三個豎立的矩形稜柱中的每一個都對應於編碼向量 $\mathbf{e}_{1}, \mathbf{e}_{2}, \mathbf{e}_{49}$，但我們可以看到這49個編碼向量被分成7行，每行7個向量。現在的想法是隻使用7個編碼向量中的一行，並將這些向量擴充套件到其他6行，本質上是重用它們的值。由於不鼓勵不同編碼向量具有相同的值，因此每個維度（又稱高度）為config.hidden_size=4的向量被切割成大小為 $1$ 的下編碼向量 $\mathbf{e}_\text{down}$ 和大小為 $3$ 的上編碼向量 $\mathbf{e}_\text{up}$，這樣下部分可以沿行維度擴充套件，上部分可以沿列維度擴充套件。讓我們透過視覺化來更清楚地瞭解。

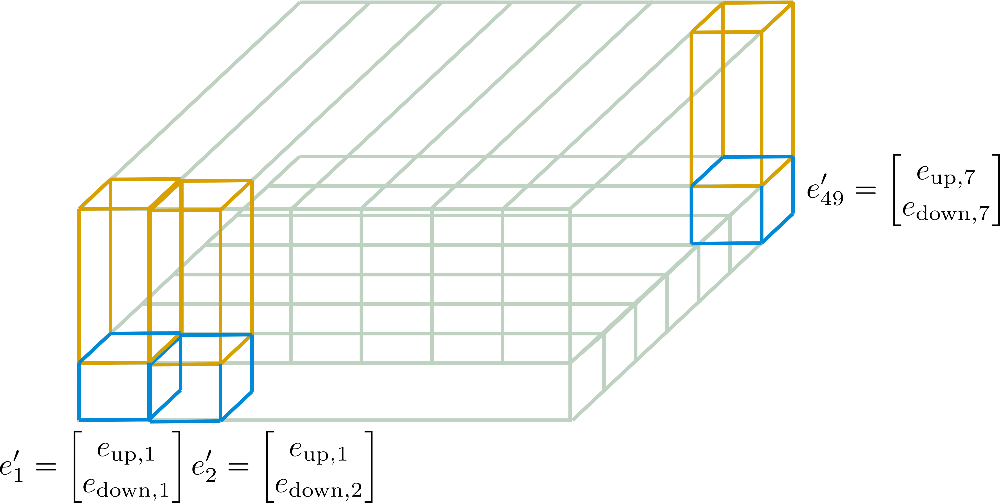
我們可以看到，我們將嵌入向量切割成 $\mathbf{e}_\text{down}$（藍色部分）和 $\mathbf{e}_\text{up}$（黃色部分）。現在，對於“子”向量 $\mathbf{E}_\text{down} = \left[\mathbf{e}_{\text{down},1}, \ldots, \mathbf{e}_{\text{down},49}\right]$，只保留了第一行（即圖中的寬度）的 $7$ 個向量，並沿列維度（即圖的深度）進行擴充套件。反之，對於“子”向量 $\mathbf{E}_\text{up} = \left[\mathbf{e}_{\text{up},1}, \ldots, \mathbf{e}_{\text{up},49}\right]$，只保留了第一列的 $7$ 個向量，並沿行維度進行擴充套件。結果得到的嵌入向量 $\mathbf{e'}_{i}$ 則對應於

$$\mathbf{e'}_{i} = \left[ \left[\mathbf{e}_{\text{down, } i \% n_\text{max}^1}\right]^T, \left[\mathbf{e}_{\text{up, } \left \lfloor{\frac{i}{{n}^2_{\text{max}}}}\right \rfloor} \right]^T \right]^T$$

其中在我們的例子中 $n_\text{max}^1 = 7$ 和 $n_\text{max}^2 = 7$。這些新的編碼 $\mathbf{E'} = \left[\mathbf{e'}_{1}, \ldots, \mathbf{e'}_{n_\text{max}}\right]$ 被稱為 **軸向位置編碼**。

下面將更詳細地說明我們示例中的這些軸向位置編碼。

現在應該更容易理解最終位置編碼向量 $\mathbf{E'}$ 是如何僅從維度為 $d_{h}^1 \times n_{\text{max}^1}$ 的 $\mathbf{E}_{\text{down}}$ 和維度為 $d_{h}^2 \times n_{\text{max}}^2$ 的 $\mathbf{E}_{\text{up}}$ 計算得出的。

這裡需要注意的關鍵一點是，軸向位置編碼確保向量 $\left[\mathbf{e'}_1, \ldots, \mathbf{e'}_{n_{\text{max}}}\right]$ 在設計上彼此相等，並且編碼矩陣的總體大小從 $n_{\text{max}} \times d_{h}$ 減少到 $n_{\text{max}}^1 \times d_{h}^1 + n_\text{max}^2 \times d_{h}^2$。透過讓每個軸向位置編碼向量在設計上不同，模型在學習高效位置表示方面獲得了更大的靈活性，如果軸向位置編碼由模型學習的話。

為了展示大小的顯著減小，我們假設對於一個可以處理高達50萬個token長度輸入的Reform模型，我們將config.axial_pos_shape = [1024, 512]和config.axial_pos_embds_dim = [512, 512]。結果得到的軸向位置編碼矩陣的大小將僅為 $1024 \times 512 + 512 \times 512 \sim 800K$ 個引數，大約相當於3MB。與此案例中標準位置編碼矩陣所需的2GB相比，這是一個巨大的減少。

有關更簡潔和數學密集的解釋，請參閱 🤗Transformers 文件 此處。

基準測試

最後，我們還將比較傳統位置嵌入和軸向位置嵌入的峰值記憶體消耗。

#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml

from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments, ReformerModel

位置嵌入僅依賴於兩個配置引數：輸入序列的最大允許長度 config.max_position_embeddings 和 config.hidden_size。讓我們使用一個將輸入序列最大允許長度推至五十萬個token的模型，名為 google/reformer-crime-and-punishment，以檢視使用軸向位置嵌入的效果。

首先，我們將比較軸向位置編碼的形狀與標準位置編碼以及模型中的引數數量。

config_no_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=False)  # disable axial positional embeddings
config_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=True, axial_pos_embds_dim=(64, 192), axial_pos_shape=(512, 1024))  # enable axial positional embeddings

print("Default Positional Encodings")
print(20 * '-')
model = ReformerModel(config_no_pos_axial_embeds)
print(f"Positional embeddings shape: {model.embeddings.position_embeddings}")
print(f"Num parameters of model: {model.num_parameters()}")
print(20 * '-' + '\n\n')

print("Axial Positional Encodings")
print(20 * '-')
model = ReformerModel(config_pos_axial_embeds)
print(f"Positional embeddings shape: {model.embeddings.position_embeddings}")
print(f"Num parameters of model: {model.num_parameters()}")
print(20 * '-' + '\n\n')

HBox(children=(FloatProgress(value=0.0, description='Downloading', max=1151.0, style=ProgressStyle(description…



Default Positional Encodings
--------------------
Positional embeddings shape: PositionEmbeddings(
  (embedding): Embedding(524288, 256)
)
Num parameters of model: 136572416
--------------------


Axial Positional Encodings
--------------------
Positional embeddings shape: AxialPositionEmbeddings(
  (weights): ParameterList(
      (0): Parameter containing: [torch.FloatTensor of size 512x1x64]
      (1): Parameter containing: [torch.FloatTensor of size 1x1024x192]
  )
)
Num parameters of model: 2584064
--------------------

閱讀了理論後，軸向位置編碼權重的形狀對於讀者來說應該不足為奇。

關於結果，可以看出，對於能夠處理如此長輸入序列的模型，使用預設位置編碼是不切實際的。在 `google/reformer-crime-and-punishment` 的情況下，僅標準位置編碼就包含超過1億個引數。軸向位置編碼將此數字減少到僅20多萬個。

最後，我們再來比較一下推理時的記憶體需求。

benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-No-Axial-Pos-Embeddings", "Reformer-Axial-Pos-Embeddings"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_pos_axial_embeds, config_pos_axial_embeds], args=benchmark_args)
result = benchmark.run()

1 / 2
2 / 2

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
Reformer-No-Axial-Pos-Embeddin       8              512             959      
Reformer-Axial-Pos-Embeddings        8              512             447      
--------------------------------------------------------------------------------

可以看出，在使用 google/reformer-crime-and-punishment 的情況下，軸向位置嵌入將記憶體需求減少了大約一半。