Q-Learning 入門 第 1 部分
Hugging Face 🤗 深度強化學習課程第二單元,第一部分
⚠️ 本文的**新更新版本可在此處獲取** 👉 https://huggingface.co/deep-rl-course/unit1/introduction
本文是深度強化學習課程的一部分。這是一個從入門到精通的免費課程。請在此處檢視課程大綱 here.

⚠️ 本文的**新更新版本可在此處獲取** 👉 https://huggingface.co/deep-rl-course/unit1/introduction
本文是深度強化學習課程的一部分。這是一個從入門到精通的免費課程。請在此處檢視課程大綱 here.
在本課程的第一章中,我們學習了強化學習 (RL)、RL 過程以及解決 RL 問題的不同方法。我們還訓練了我們的第一個著陸器智慧體,使其**成功降落在月球🌕上,並將其上傳到 Hugging Face Hub。**
所以今天,我們將**深入探討強化學習方法之一:基於價值的方法**,並學習我們的第一個 RL 演算法:**Q-學習。**
我們還將**從頭開始實現我們的第一個 RL 智慧體**:一個 Q-學習智慧體,並將在兩個環境中訓練它。
- Frozen-Lake-v1(非滑溜版本):我們的智慧體需要**從起始狀態 (S) 到目標狀態 (G)**,只在冰凍的瓷磚 (F) 上行走並避開洞 (H)。
- 一輛自動駕駛出租車需要**學習導航**城市,以**將其乘客從 A 點運送到 B 點。**
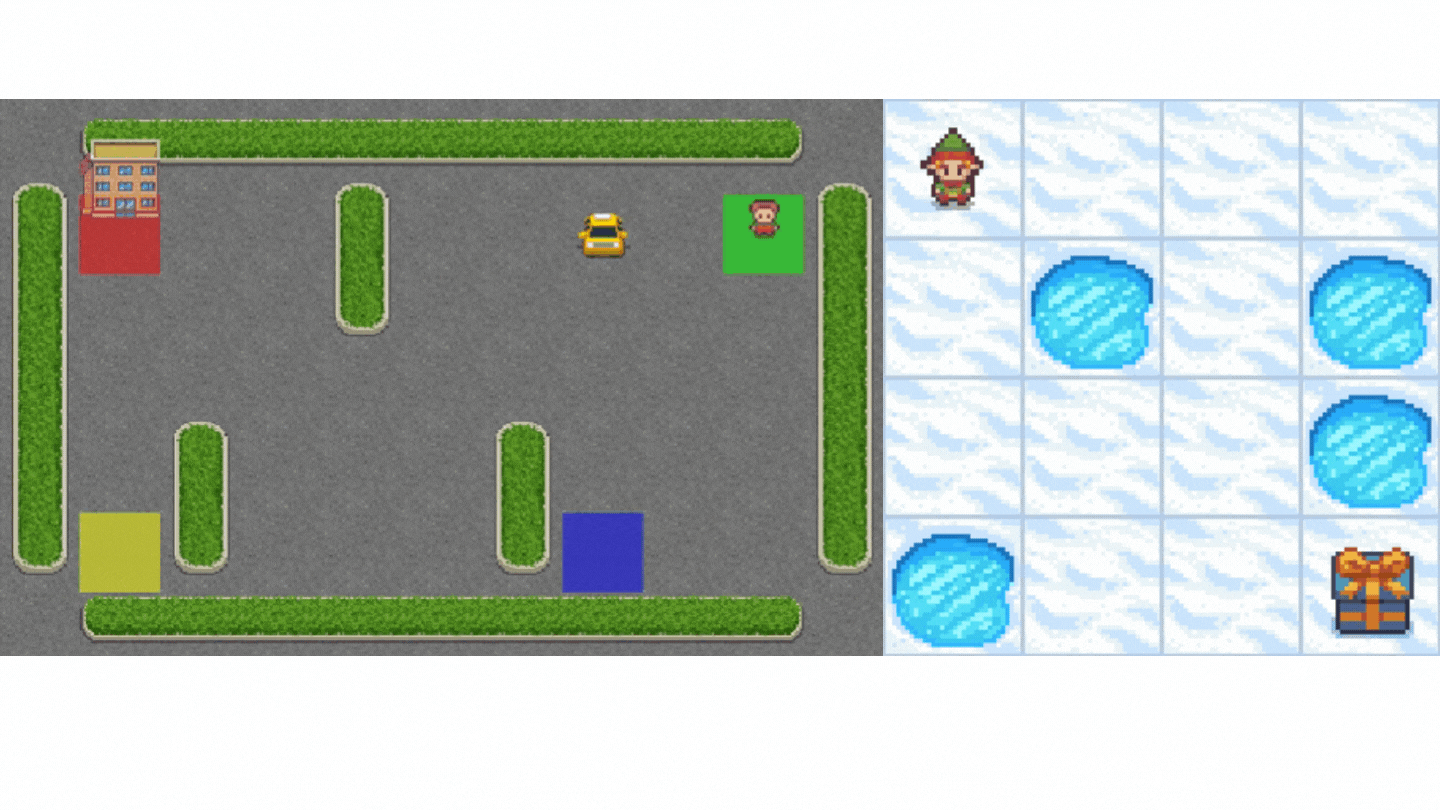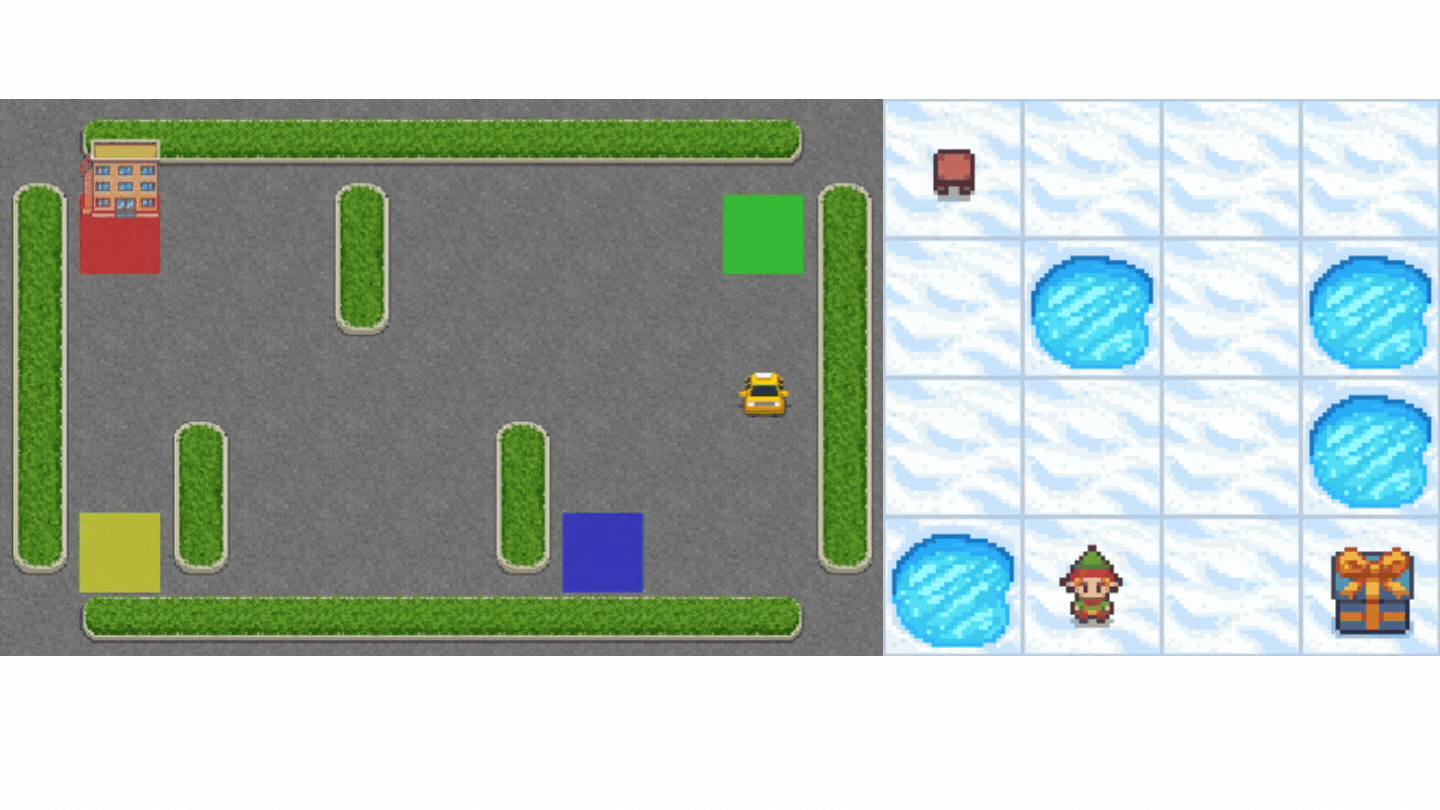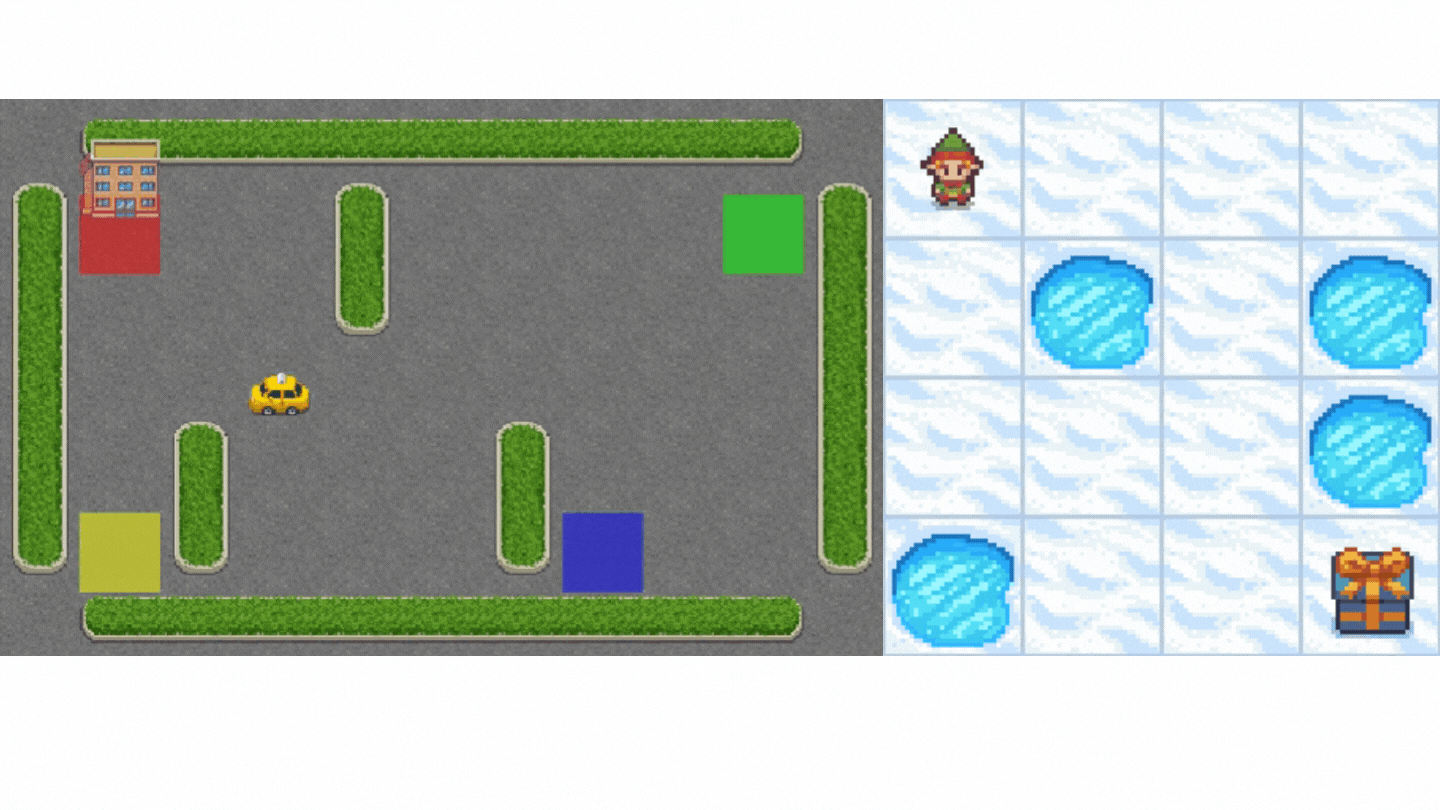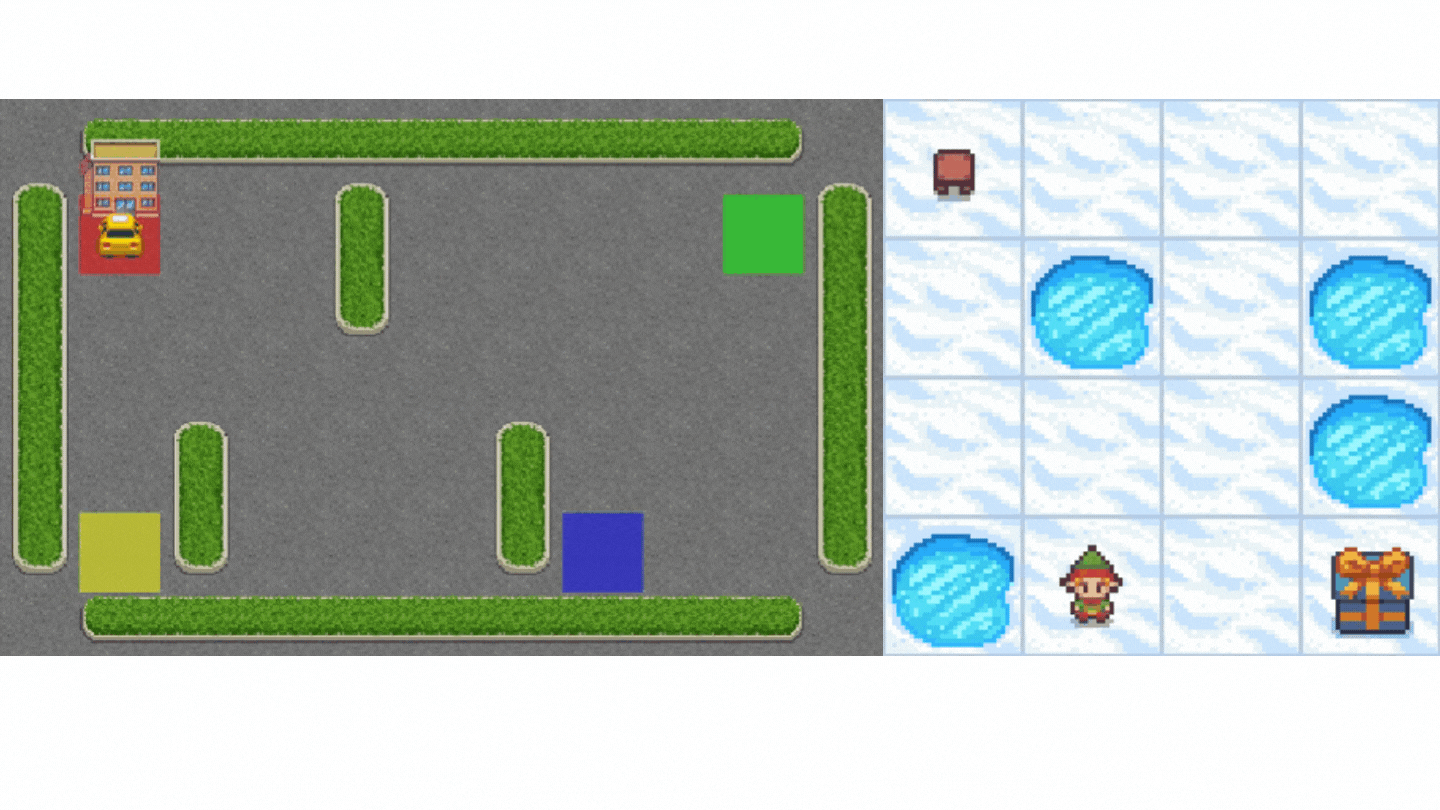
本單元分為 2 部分。
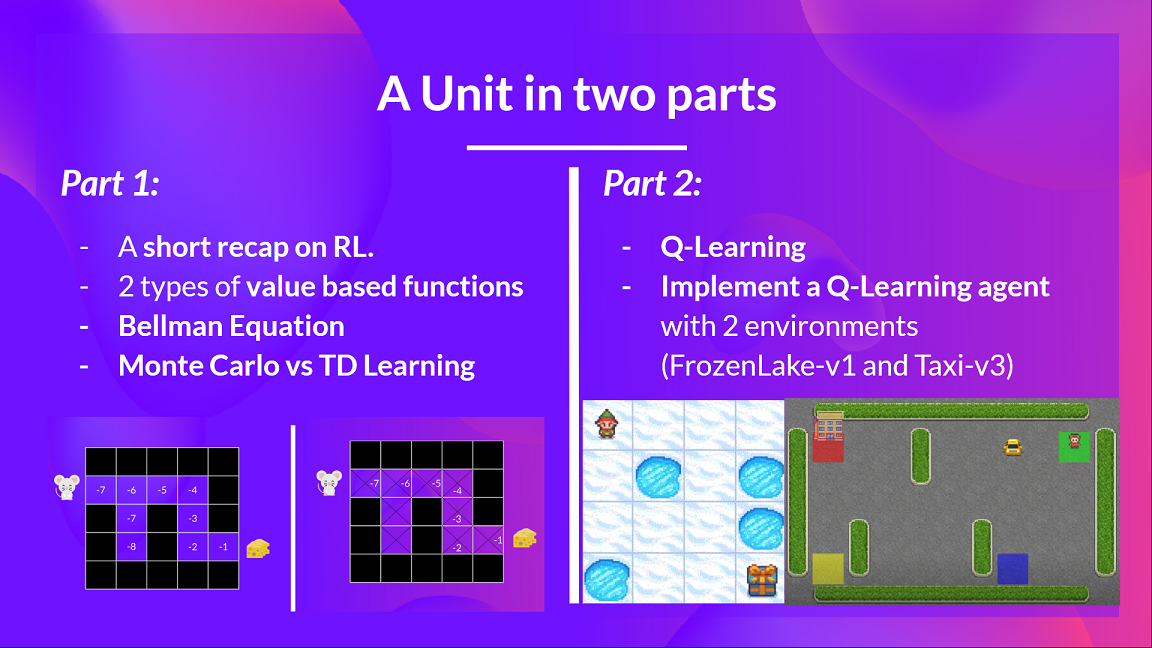
在第一部分中,我們將**學習基於價值的方法以及蒙特卡羅和時序差分學習之間的區別。**
在第二部分中,**我們將學習我們的第一個 RL 演算法:Q-學習,並實現我們的第一個 RL 智慧體。**
**如果你想深入研究深度 Q-學習**(第三單元),本單元至關重要:深度 Q-學習是第一個能夠玩 Atari 遊戲並在其中一些遊戲(Breakout、Space Invaders 等)中**擊敗人類水平**的深度 RL 演算法。
那麼,讓我們開始吧!
**什麼是強化學習?簡短回顧**
在強化學習中,我們構建一個可以**做出明智決策**的智慧體。例如,一個**學習翫影片遊戲**的智慧體。或者一個交易智慧體,透過**做出買賣股票的明智決策**來**最大化其收益**。
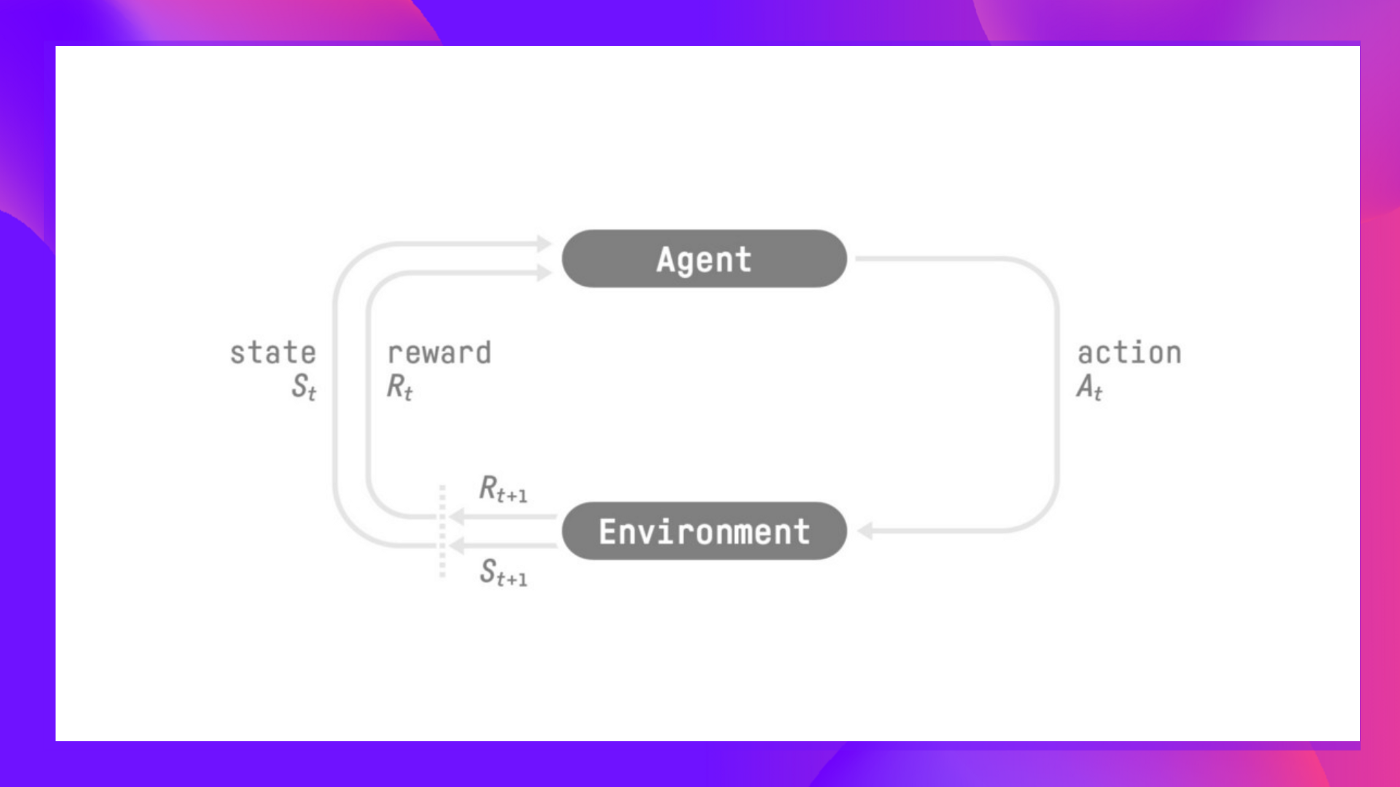
但是,為了做出智慧決策,我們的智慧體將透過**試錯**與環境互動來學習,並獲得(正面或負面)獎勵作為**獨特的反饋。**
其目標**是最大化其預期的累積獎勵**(根據獎勵假設)。
**智慧體的決策過程稱為策略 π:**給定一個狀態,策略將輸出一個動作或一個動作的機率分佈。也就是說,給定環境的觀察,策略將提供智慧體應該採取的動作(或每個動作的多個機率)。

**我們的目標是找到一個最優策略 π** *,即,一個能夠帶來最佳預期累積獎勵的策略。
為了找到這個最優策略(從而解決強化學習問題),**有兩種主要的強化學習方法。**
- _基於策略的方法_:**直接訓練策略**,以學習在給定狀態下采取哪個動作。
- _基於價值的方法_:**訓練一個價值函式**,以學習**哪個狀態更有價值**,並使用這個價值函式**來採取導致該價值的動作。**

在本章中,**我們將深入探討基於價值的方法。**
**兩種基於價值的方法**
在基於價值的方法中,**我們學習一個價值函式**,它**將狀態對映到在該狀態下的預期價值。**

一個狀態的價值是智慧體**從該狀態開始**並根據我們的策略行動後可以獲得的**預期折扣回報**。
如果你忘記了什麼是折扣,你可以閱讀這一節。
但是,根據我們的策略行動是什麼意思呢?畢竟,在基於價值的方法中我們沒有策略,因為我們訓練的是價值函式而不是策略。
請記住,**RL 智慧體的目標是擁有一個最優策略 π。**
為了找到它,我們瞭解到有兩種不同的方法。
- _基於策略的方法:_**直接訓練策略**,以選擇在給定狀態下采取哪個動作(或在該狀態下動作的機率分佈)。在這種情況下,我們**沒有價值函式。**
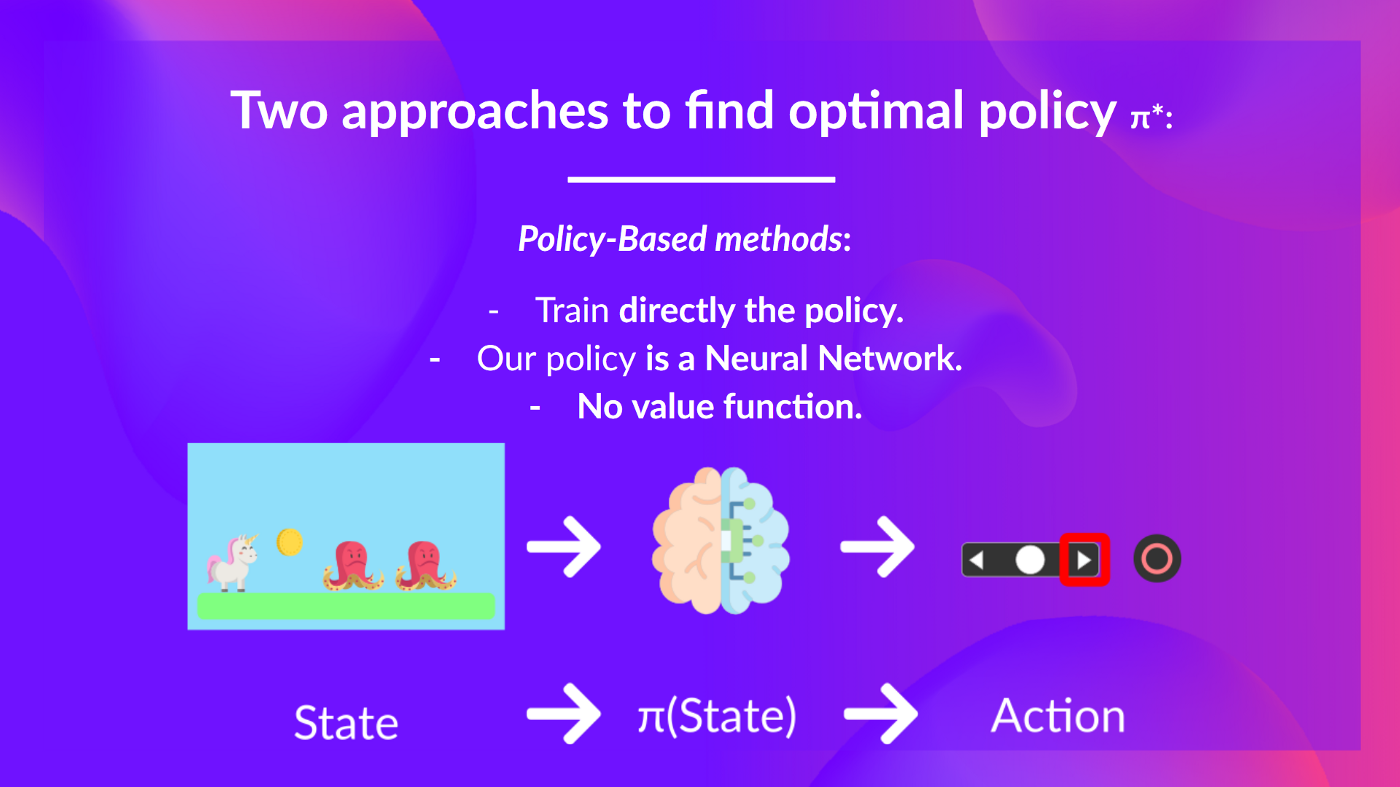
策略以狀態作為輸入,並輸出在該狀態下要採取的動作(確定性策略)。
因此,**我們不需要手動定義策略的行為;訓練將定義它。**
- _基於價值的方法:_**間接地,透過訓練一個價值函式**,該函式輸出狀態或狀態-動作對的價值。給定此價值函式,我們的策略**將採取行動。**
但是,因為我們沒有訓練我們的策略,**我們需要指定其行為。**例如,如果我們需要一個策略,在給定價值函式的情況下,它將總是採取導致最大獎勵的動作,**我們將建立一個貪婪策略。**

因此,無論您使用哪種方法解決問題,**您都會有一個策略**,但在基於價值的方法中,您不訓練它,您的策略**只是一個您指定的簡單函式**(例如貪婪策略),並且此策略**使用價值函式給出的值來選擇其動作。**
所以區別在於:
- 在基於策略的方法中,**透過直接訓練策略來找到最優策略。**
- 在基於價值的方法中,**找到一個最優價值函式會導致擁有一個最優策略。**

事實上,在大多數情況下,基於價值的方法會使用**一個 Epsilon-Greedy 策略**來處理探索/利用的權衡;我們將在本單元的第二部分討論 Q-Learning 時詳細說明。
所以,我們有兩種基於價值的函式:
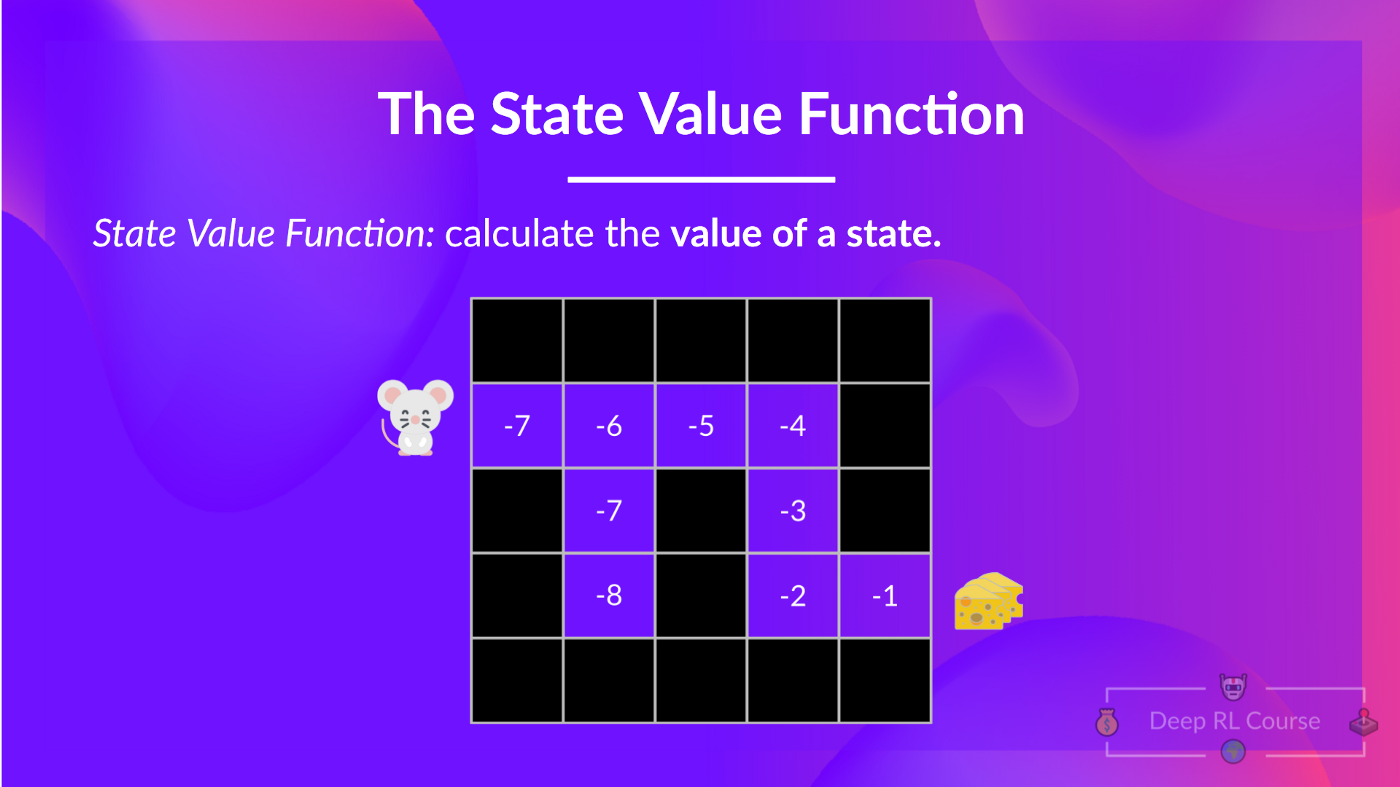
**狀態價值函式**
我們這樣寫策略 π 下的狀態價值函式:
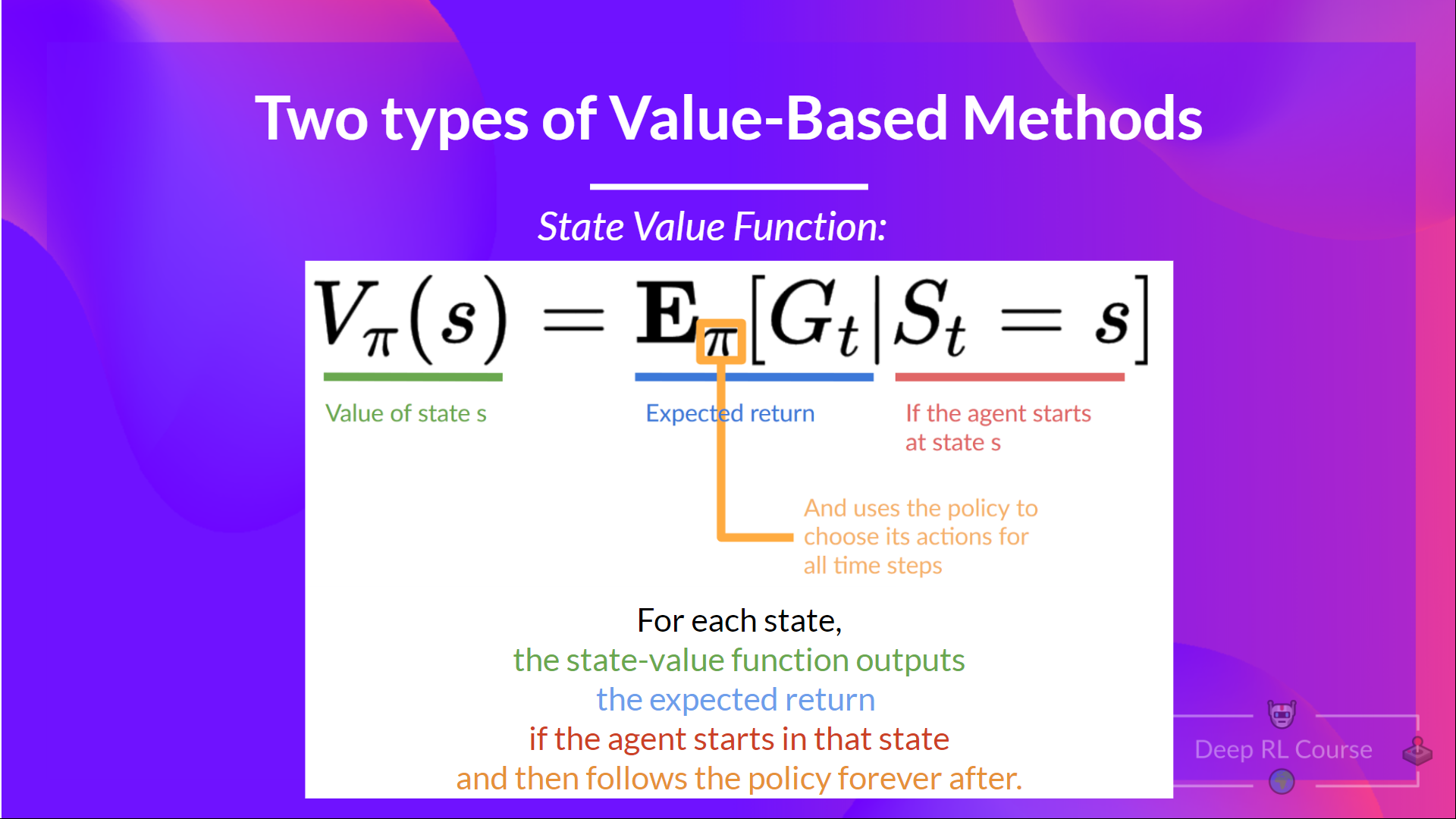
對於每個狀態,狀態價值函式輸出預期回報,如果智慧體**從該狀態開始**,然後永遠遵循該策略(如果你喜歡,對於所有未來的時間步)。
**動作價值函式**
在動作價值函式中,對於每個狀態和動作對,動作價值函式輸出預期回報,如果智慧體從該狀態開始並採取動作,然後永遠遵循該策略。
在策略 π 下,在狀態 s 採取動作 a 的價值是


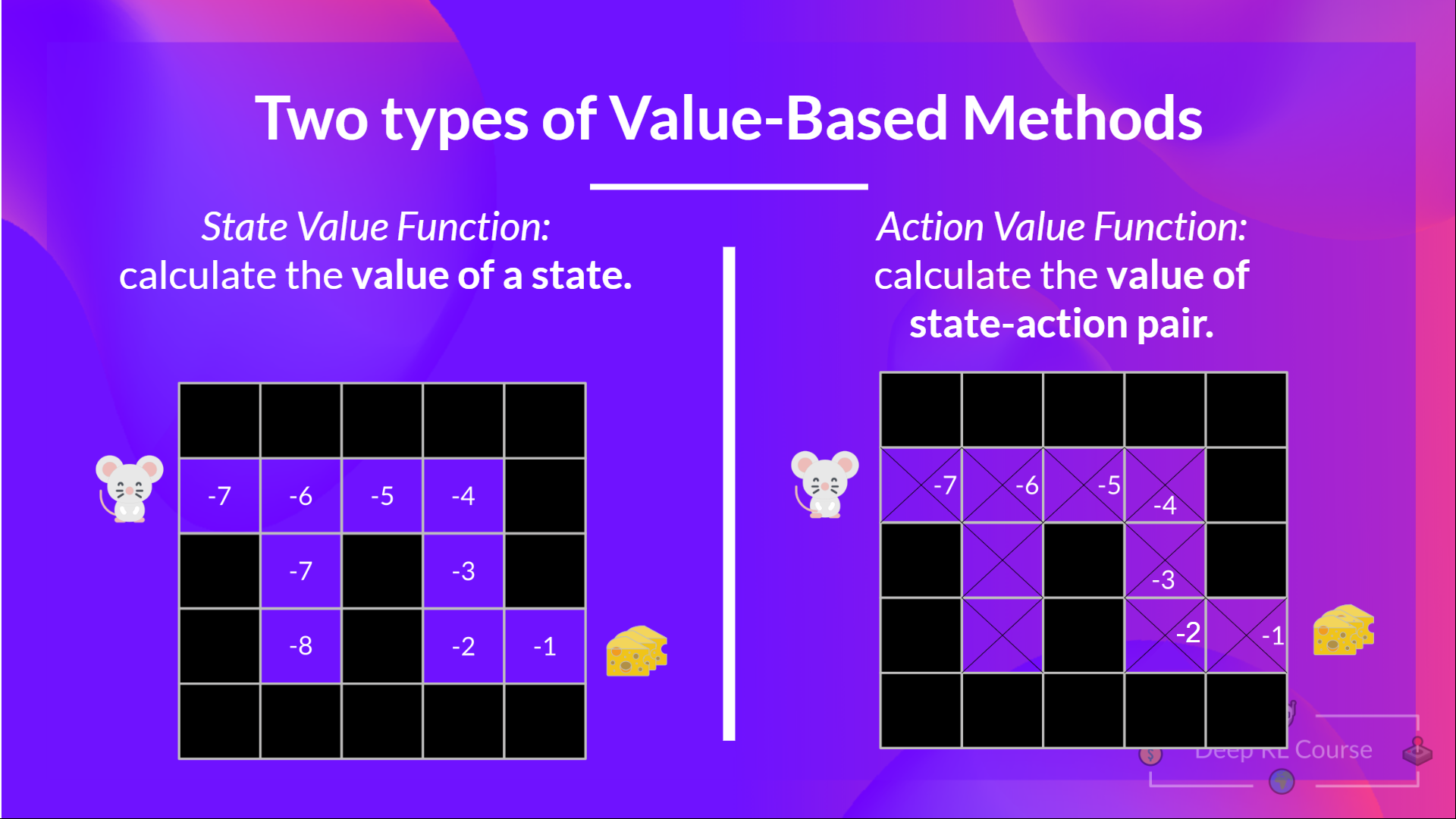
我們看到區別在於:
- 在狀態價值函式中,我們計算**狀態 **的價值。
- 在動作價值函式中,我們計算**狀態-動作對( )的價值,因此是採取該動作在該狀態下的價值。**
無論我們選擇哪種價值函式(狀態價值或動作價值函式),**價值都是預期回報。**
然而,問題在於,這意味著**要計算一個狀態或一個狀態-動作對的每個價值,我們需要對智慧體從該狀態開始可以獲得的所有獎勵進行求和。**
這可能是一個繁瑣的過程,而這正是**貝爾曼方程幫助我們的地方。**
**貝爾曼方程:簡化我們的價值估計**
貝爾曼方程**簡化了我們的狀態價值或狀態-動作價值計算。**

根據我們目前所學,我們知道如果計算 (一個狀態的價值),我們需要計算從該狀態開始並永遠遵循策略的回報。(**在以下示例中,我們定義的策略是貪婪策略,為了簡化,我們不對獎勵進行折扣**)。
因此,要計算 ,我們需要對預期獎勵求和。因此:
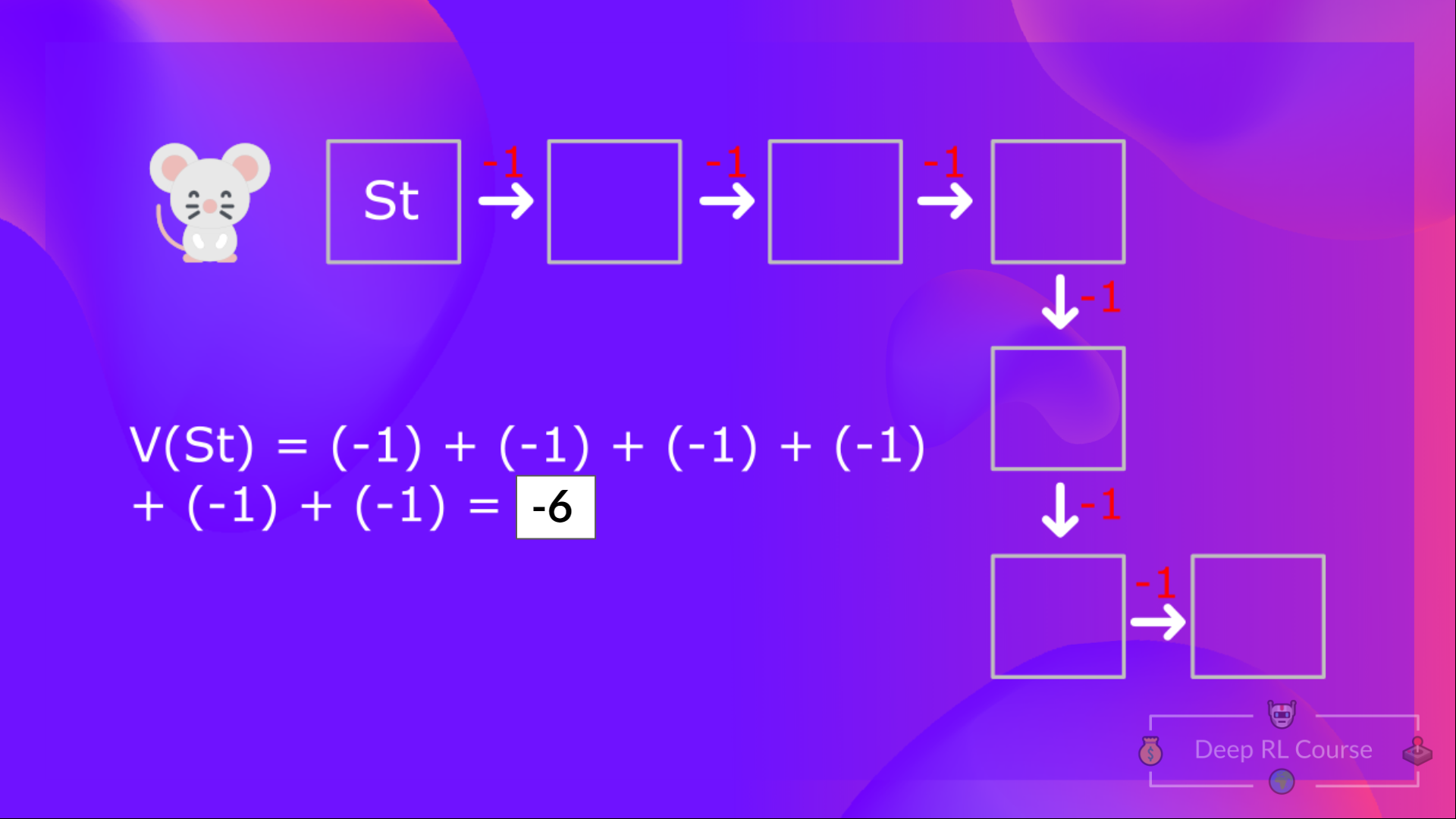
然後,要計算 ,我們需要計算從狀態 開始的回報。
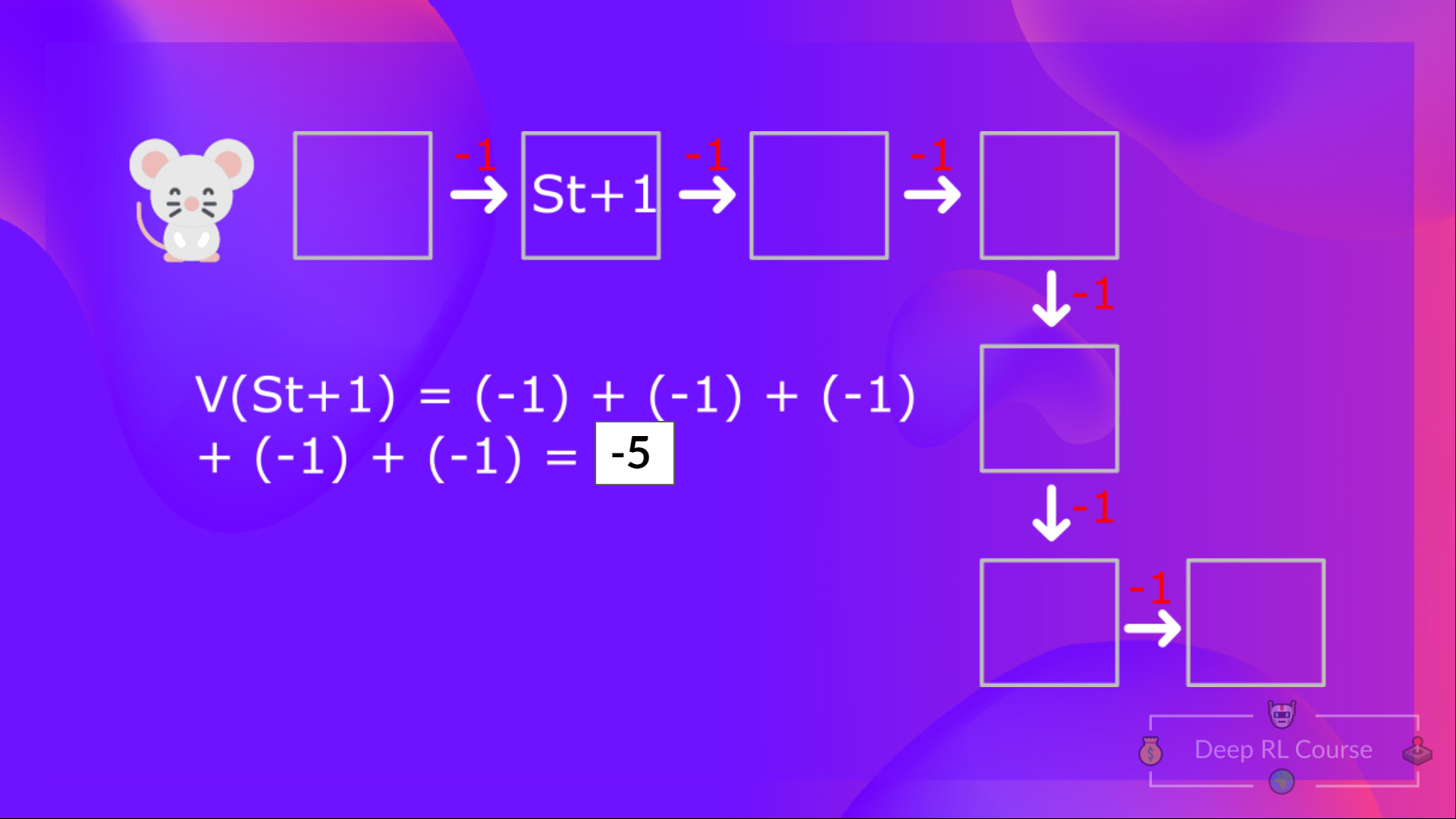
所以你看,如果你需要對每個狀態值或狀態-動作值都這樣做,那將是一個非常繁瑣的過程。
與其計算每個狀態或每個狀態-動作對的預期回報,**我們可以使用貝爾曼方程。**
貝爾曼方程是一個遞迴方程,其工作原理如下:我們不再從頭開始計算每個狀態的價值並計算回報,而是將任何狀態的價值視為:
即時獎勵 + 後續狀態的折扣值( )。

如果回到我們的例子,狀態 1 的價值 = 如果我們從該狀態開始,預期的累積回報。

為了計算狀態 1 的價值:**如果智慧體從狀態 1 開始**,然後**在所有時間步長中都遵循策略**,則獎勵的總和。
這等價於 = 即時獎勵 + 下一個狀態的折扣值
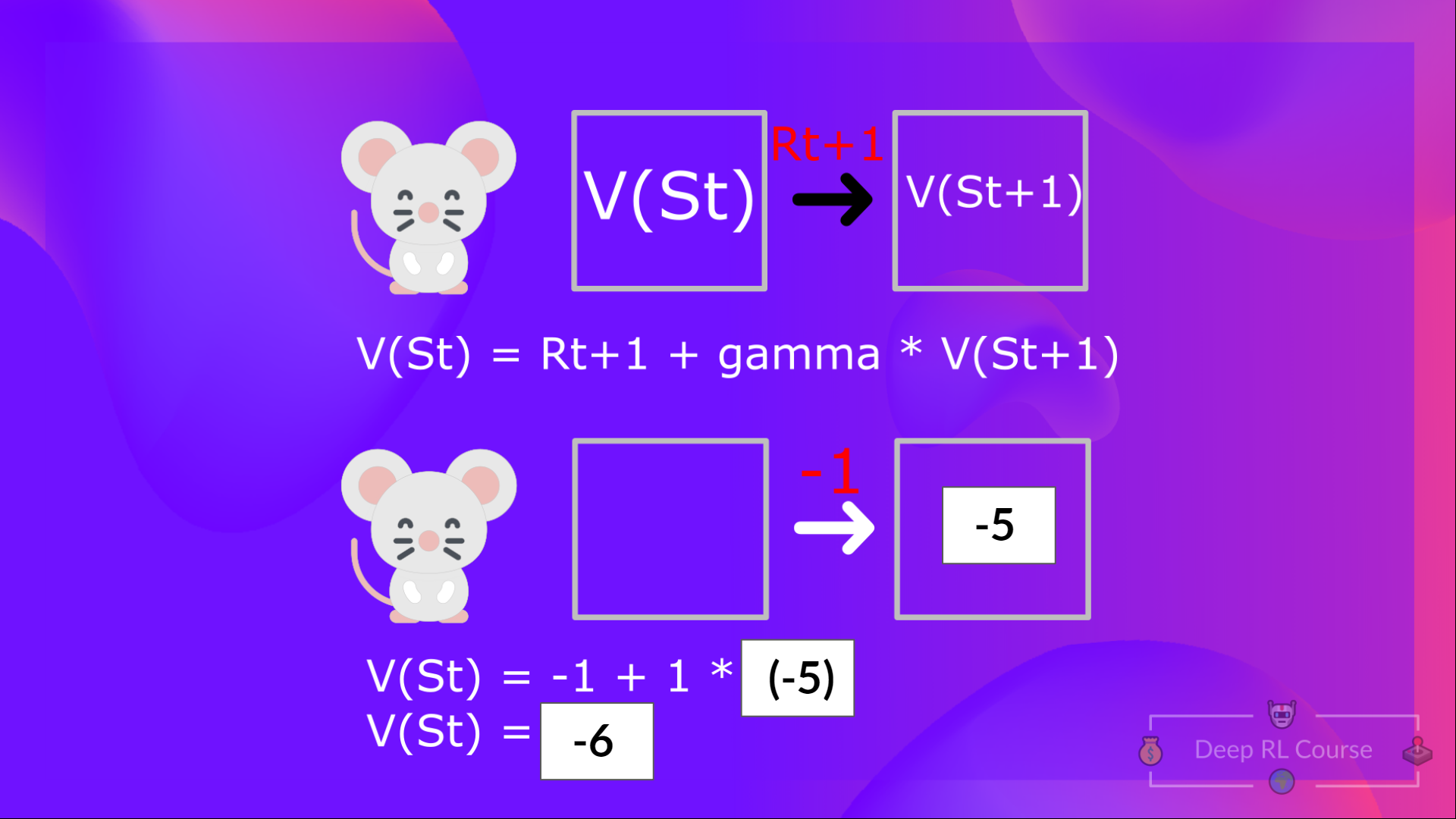
為簡化起見,這裡我們不打折,所以伽馬 = 1。
- 的值 = 即時獎勵 + 下一個狀態的折扣值( )。
- 等等。
總結一下,貝爾曼方程的理念是,不再將每個值計算為預期回報的總和,**這是一個漫長的過程。**這等價於**即時獎勵 + 下一個狀態的折扣值的總和。**
**蒙特卡羅 vs. 時序差分學習**
在深入 Q-Learning 之前,我們需要談論的最後一件事是兩種學習方式。
請記住,RL 智慧體**透過與環境互動來學習。**其理念是,**利用獲得的經驗**,根據獲得的獎勵,**更新其價值或策略。**
蒙特卡羅和時序差分學習是兩種不同的**訓練我們的價值函式或策略函式的方法。**它們都**利用經驗來解決強化學習問題。**
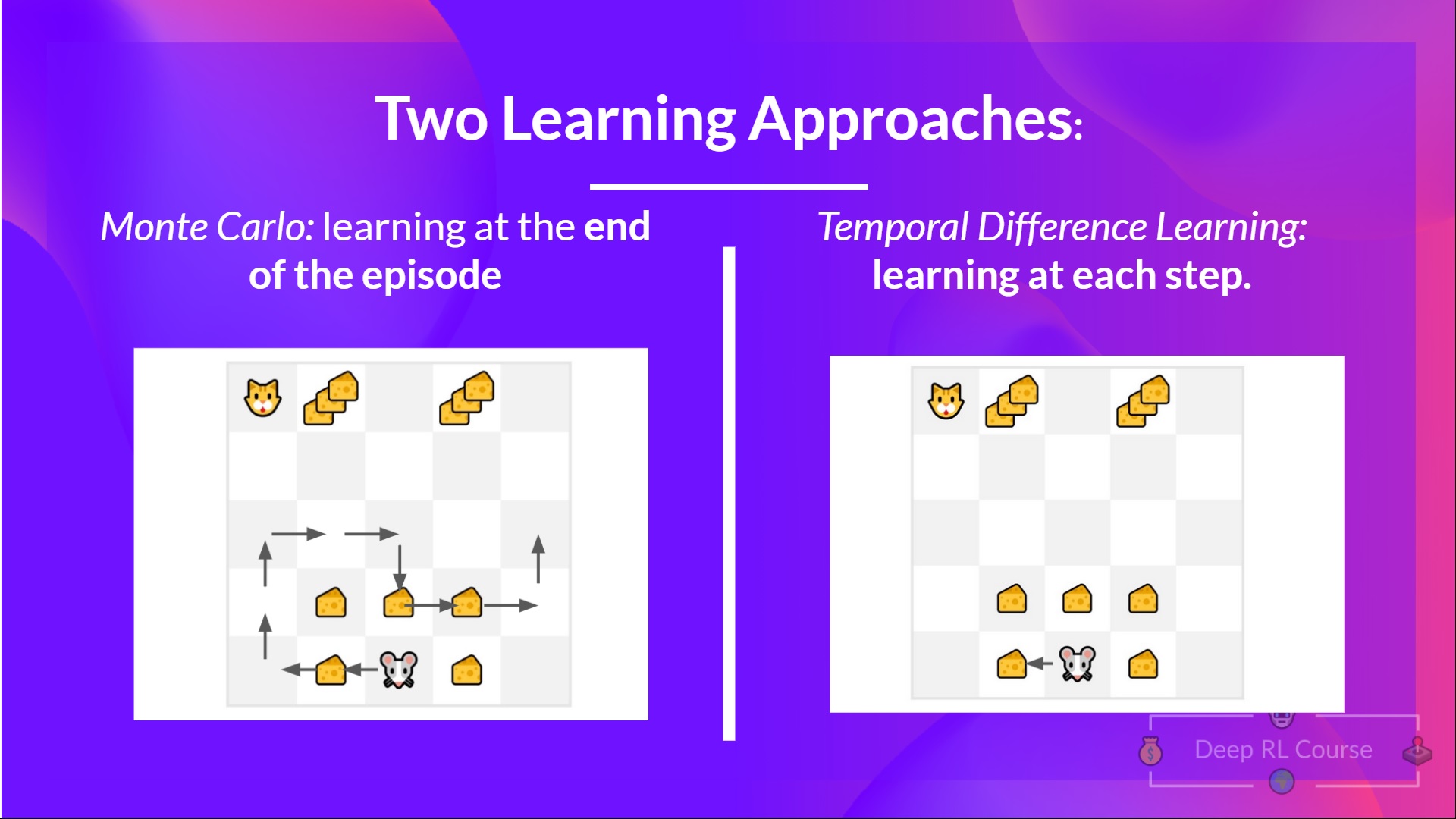
一方面,蒙特卡羅在學習之前使用**整個回合的經驗。**另一方面,時序差分只使用**一個步驟( )來學習。**
我們將透過**一個基於價值的方法示例**來解釋兩者。
**蒙特卡羅:在回合結束時學習**
蒙特卡羅會等到回合結束,計算 (回報),並將其用作**更新 的目標。**
因此,它需要**一個完整的互動回合才能更新我們的價值函式。**

如果我們舉一個例子:
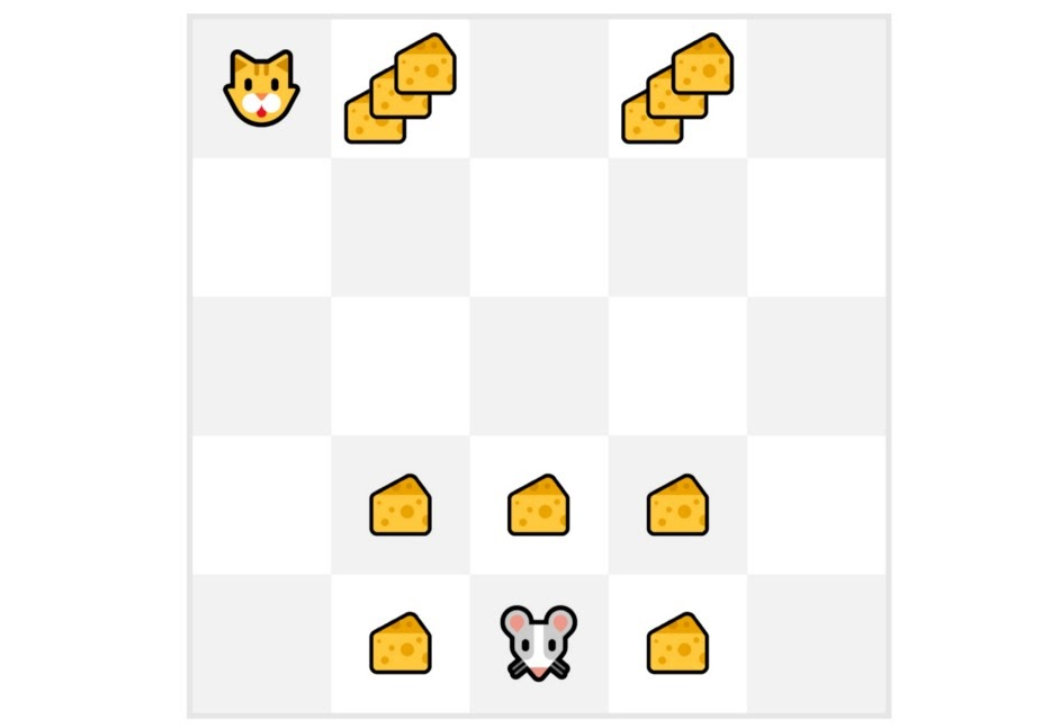
我們總是從**相同的起始點**開始一個回合。
**智慧體使用策略採取行動**。例如,使用 Epsilon 貪婪策略,它在探索(隨機行動)和利用之間交替。
我們得到**獎勵和下一個狀態。**
如果貓吃了老鼠,或者老鼠移動了 > 10 步,我們就終止這個回合。
在回合結束時,**我們有一個狀態、動作、獎勵和下一個狀態的列表**。
**智慧體將對總獎勵 進行求和**(以檢視其表現如何)。
然後它將**根據公式更新 **。

- 然後**帶著這些新知識開始新的遊戲。**
透過執行越來越多的回合,**智慧體將學會玩得越來越好。**

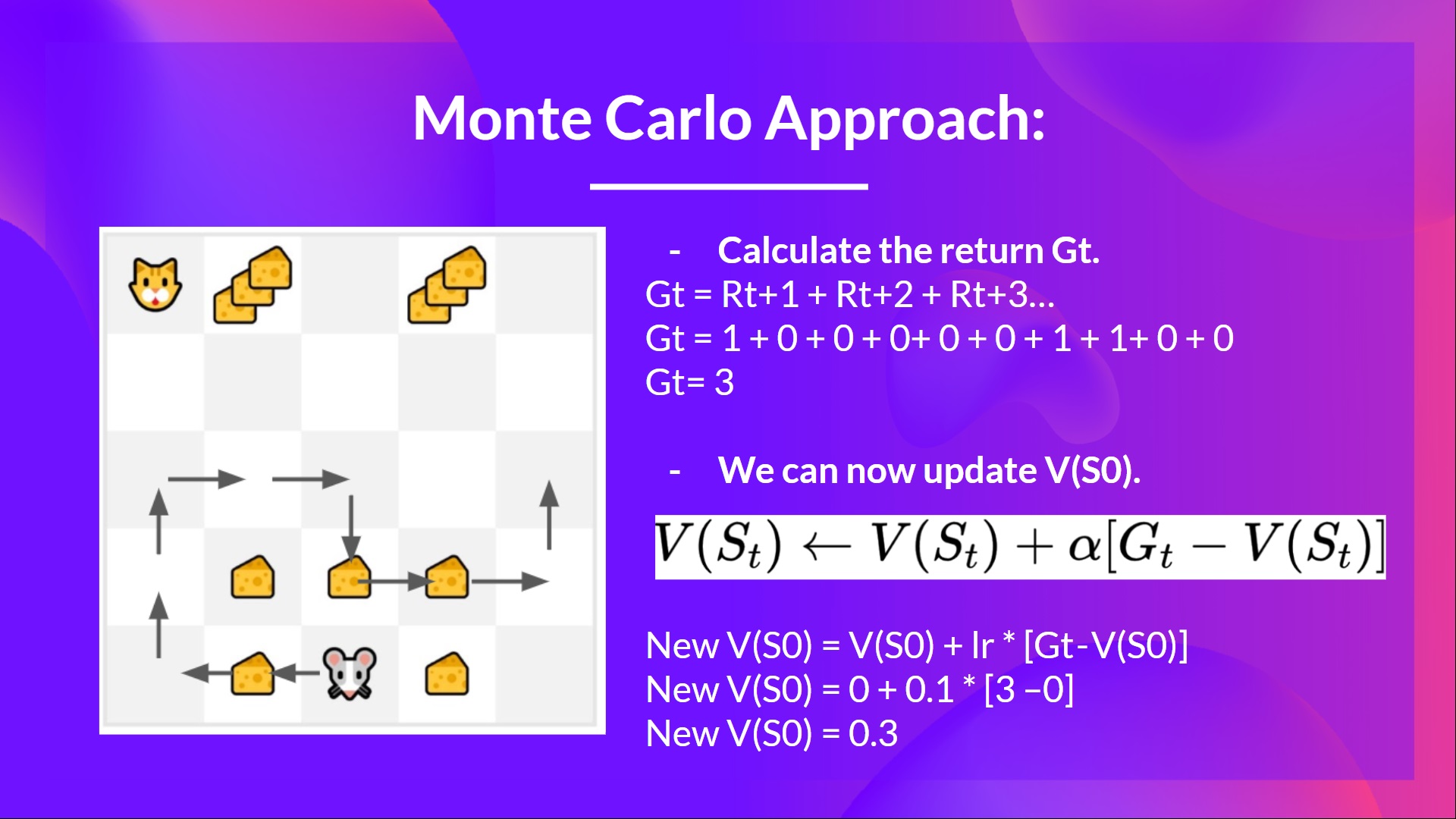
例如,如果我們使用蒙特卡羅訓練一個狀態價值函式:
- 我們剛剛開始訓練我們的價值函式,**因此它對每個狀態都返回 0 值。**
- 我們的學習率 (lr) 為 0.1,折扣率為 1(= 無折扣)。
- 我們的老鼠**探索環境並採取隨機行動**。
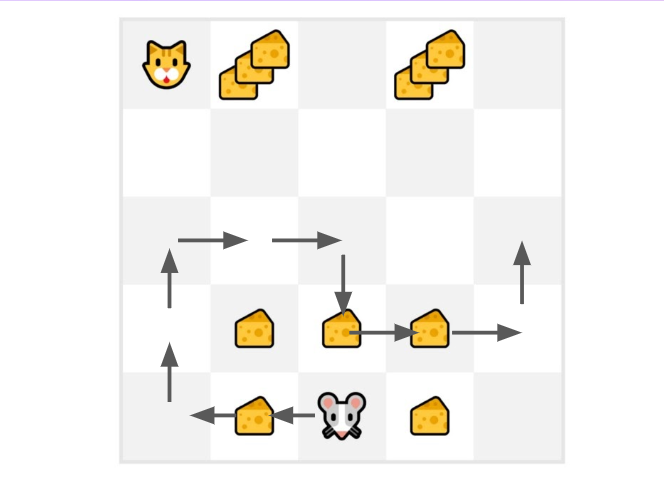
- 老鼠走了超過 10 步,所以回合結束了。
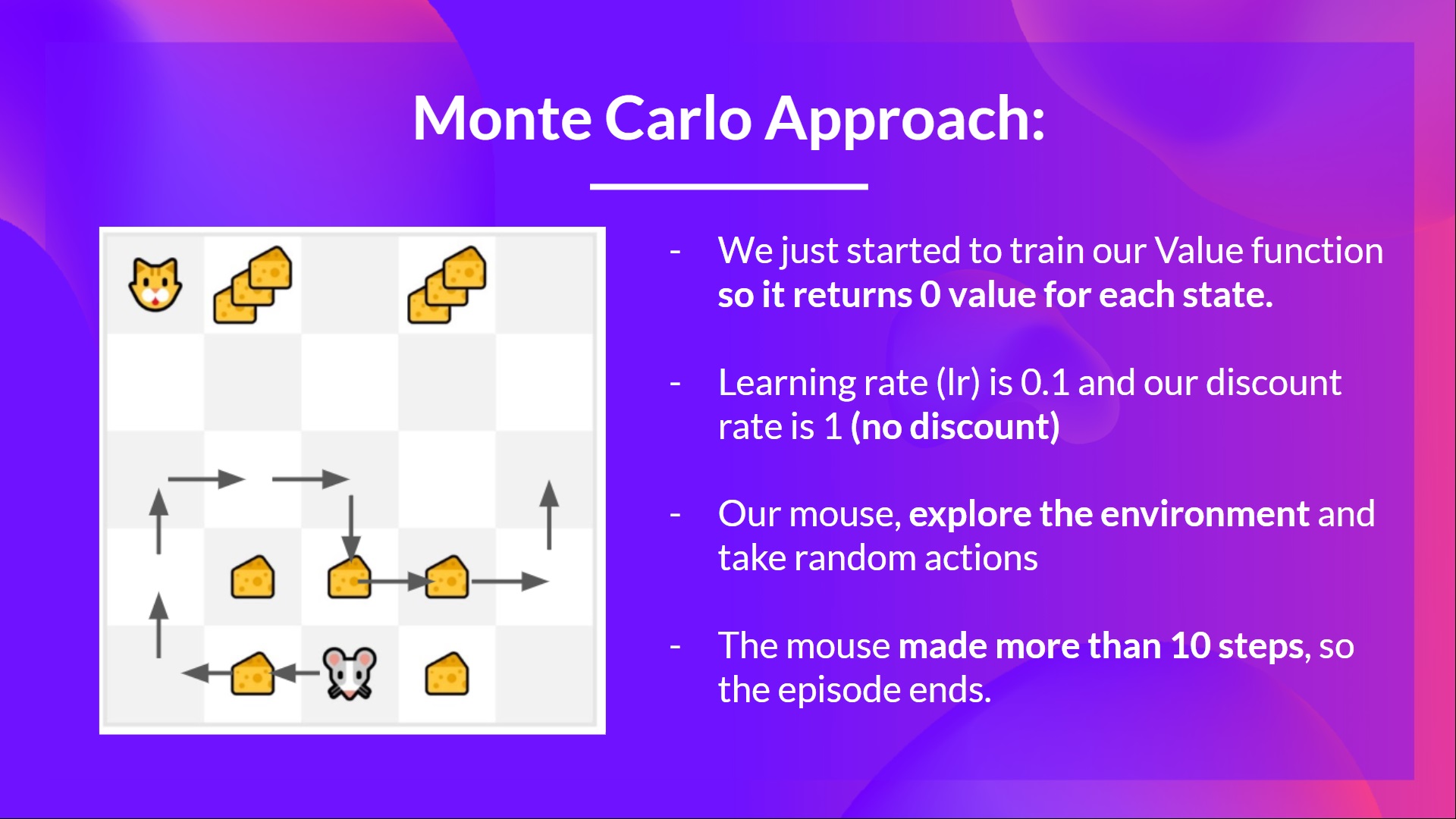
- 我們有一個狀態、動作、獎勵、下一個狀態的列表,**我們需要計算回報 **。
- (為簡單起見,我們不對獎勵進行折扣)。
- 我們現在可以更新 了。

- 新的
- 新的
- 新的
**時序差分學習:在每一步學習**
- 另一方面,時序差分只等待一次互動(一個步驟)
- 以形成一個 TD 目標,並使用 和 來更新 。
TD 的核心思想是在每一步都更新 。
但由於我們沒有在一個完整的 episode 中進行遊戲,所以我們沒有 (預期回報)。相反,我們透過將 和下一個狀態的折扣值相加來估算 。
這被稱為自舉法。之所以這樣命名,是因為 TD 更新部分是基於現有估計值 ,而不是完整的樣本 。

此方法稱為 TD(0) 或單步 TD(在任何單個步驟後更新值函式)。

如果我們採用相同的例子,

- 我們剛剛開始訓練我們的值函式,所以它為每個狀態返回 0 值。
- 我們的學習率(lr)是 0.1,我們的折扣率是 1(無折扣)。
- 我們的老鼠探索環境並採取了一個隨機行動:向左走
- 它獲得獎勵 ,因為它吃到了一塊乳酪。
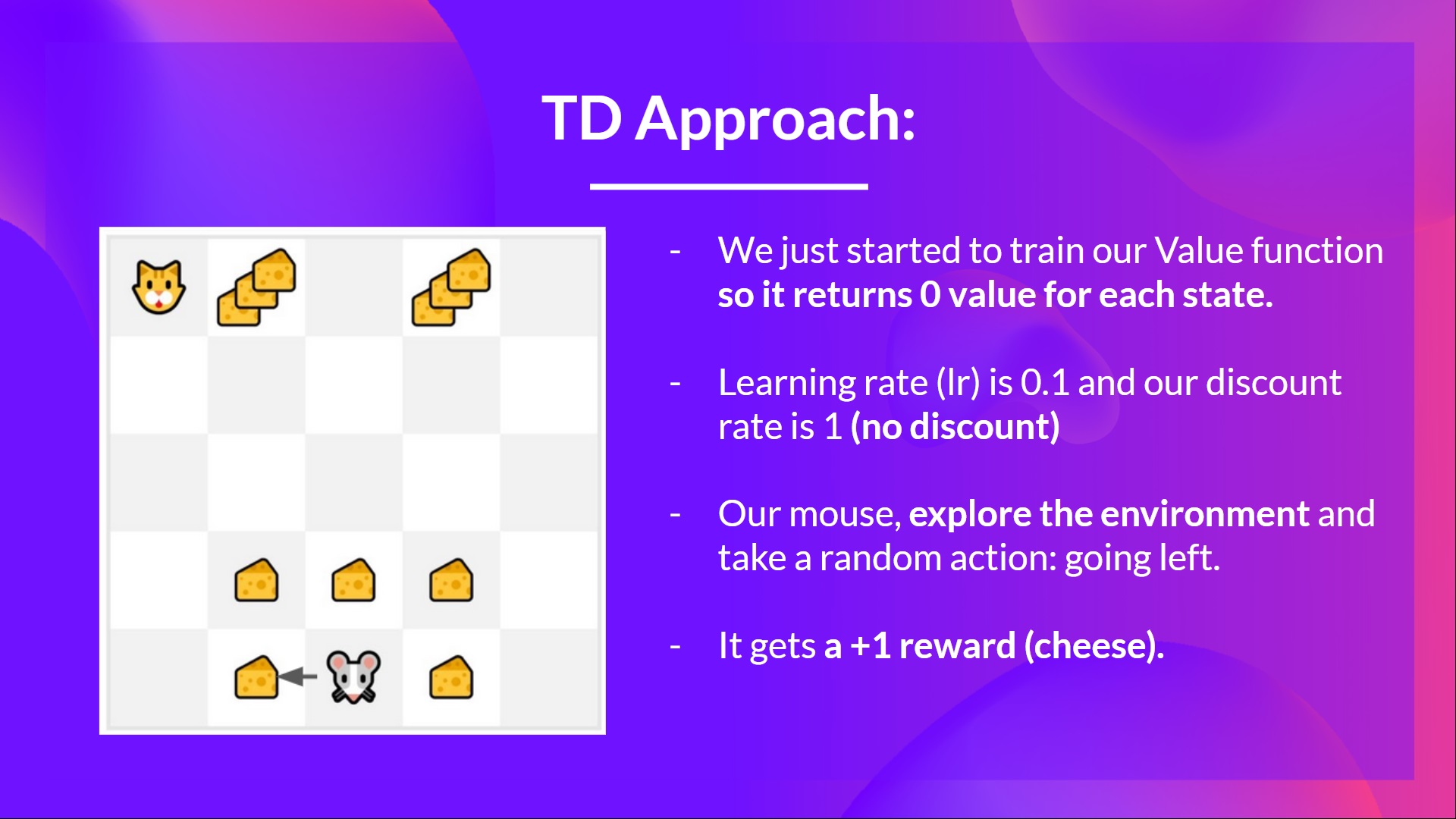
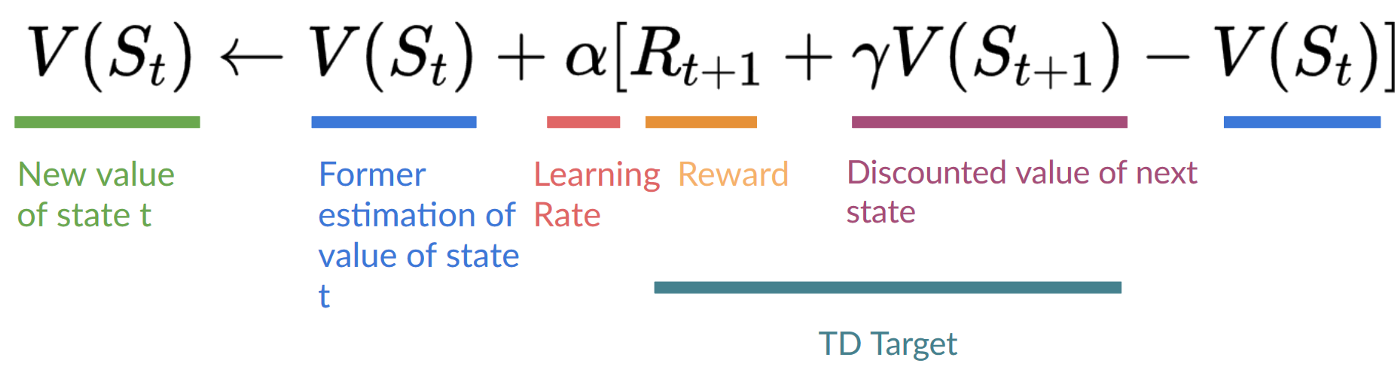
我們現在可以更新 了。
新
新
新
所以我們剛剛更新了狀態 0 的值函式。
現在,我們將繼續使用更新後的值函式與環境互動。

總結一下
- 使用蒙特卡洛方法,我們從一個完整的 episode 更新值函式,因此我們使用該 episode 實際準確的折扣回報。
- 使用 TD 學習,我們從一個步驟更新值函式,因此我們用稱為 TD 目標的估計回報替換了我們沒有的 。
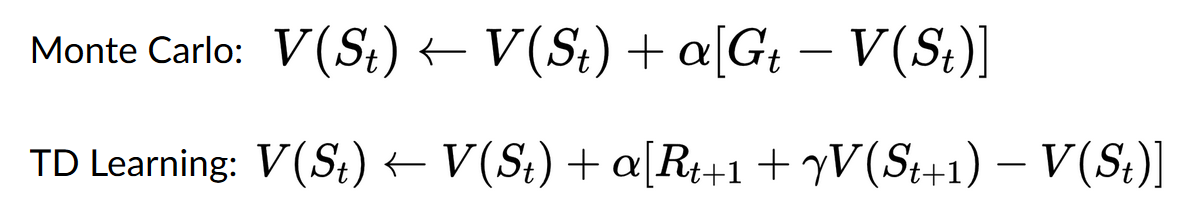
現在,在深入學習 Q-Learning 之前,讓我們總結一下我們剛剛學到的內容
我們有兩種型別的值函式
- 狀態值函式:輸出代理在給定狀態開始並始終按照策略行動時的預期回報。
- 動作值函式:輸出代理在給定狀態開始,在該狀態下采取給定動作,然後始終按照策略行動時的預期回報。
- 在基於值的方法中,我們手動定義策略,因為我們不訓練策略,我們訓練值函式。我們的想法是,如果我們有一個最優值函式,我們就會有一個最優策略。
有兩種學習值函式策略的方法
- 使用蒙特卡洛方法,我們從一個完整的 episode 更新值函式,因此我們使用該 episode 實際準確的折扣回報。
- 使用TD 學習方法,我們從一個步驟更新值函式,因此我們用稱為 TD 目標的估計回報替換了我們沒有的 Gt。
今天就到這裡。恭喜您完成本章的第一部分!資訊量很大。
如果您仍然對所有這些內容感到困惑,這是正常的。我和所有學習強化學習的人都一樣。
在繼續之前,花時間真正理解這些材料.
由於學習和避免能力錯覺的最佳方法是測試自己。我們編寫了一個小測驗來幫助您找到需要加強學習的地方。在這裡檢視您的知識 👉 https://github.com/huggingface/deep-rl-class/blob/main/unit2/quiz1.md
在第二部分中,我們將學習我們的第一個強化學習演算法:Q-Learning,並在兩個環境中實現我們的第一個強化學習代理。
- Frozen-Lake-v1(非滑溜版本):我們的智慧體需要**從起始狀態 (S) 到目標狀態 (G)**,只在冰凍的瓷磚 (F) 上行走並避開洞 (H)。
- 一輛自動駕駛出租車需要**學習導航**城市,以**將其乘客從 A 點運送到 B 點。**

別忘了分享給你想學習的朋友 🤗!
最後,我們希望**根據你的反饋不斷改進和更新課程**。如果你有任何反饋,請填寫此表格 👉 https://forms.gle/3HgA7bEHwAmmLfwh9

